Question

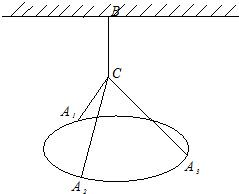一个圆环直径为2

2

m，通过铁丝BC，CA₁，CA₂，CA₃（A₁，A₂，A₃是圆上三等分点）悬挂在B处，圆环呈水平状态并距天花板2m，如图所示．
（Ⅰ）设BC长为x（m），铁丝总长为y（m），试写出y关于x的函数解析式，并写出函数定义域；
（Ⅱ）当x取多长时，铁丝总长y有最小值，并求此最小值．

Answer 1

分析：（Ⅰ）由题意C，A₁，A₂，A₃四点构成一个正三棱锥，CA₁，CA₂，CA₃为该三棱锥的三条侧棱，再利用直角三角形中的边的关系即可求得铁丝总长；
（Ⅱ）欲求铁丝总长y的最小值，先对y求导，利用导数的知识研究函数的单调性，进而求得其最小值即可解决问题．

解答：解：（Ⅰ）由题意C，A₁，A₂，A₃四点构成一个正三棱锥，CA₁，CA₂，CA₃为该三棱锥的三条侧棱．（2分）
三棱锥的侧棱CA1=

(2-x)2+2

；（4分）
于是有y=x+3

(2-x)2+2

．（0＜x＜2）（5分）
（Ⅱ）对y求导得y′=1-

3(2-x)

(2-x)2+2

．（8分）
令y'=0得9（2-x）²=（2-x）²+2，
解得x=

3

2

或x=

5

2

（舍）．（10分）
当x∈(0，

3

2

)时，y'＜0，
当x∈(

3

2

，2)时，y'＞0．（12分）
故当x=

3

2

时，即BC=1.5m时，y取得最小值为6m．（13分）

点评：本小题主要考查函数模型的选择与应用、导数在研究函数单调性上的应用及函数的最值，考查运算求解能力，考查空间想象力、化归与转化思想．属于基础题．