题目内容
设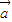 与
与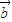 的夹角为θ,
的夹角为θ,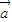 =(3,3),2
=(3,3),2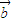 -
-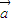 =(-1,1),则cosθ=
=(-1,1),则cosθ=
【答案】分析:设出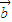 的坐标,利用2
的坐标,利用2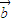 -
-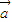 =(-1,1)求得x和y,进而求得两向量的积,和两向量的模,最后利用平面向量的数量积的法则求得cosθ的值.
=(-1,1)求得x和y,进而求得两向量的积,和两向量的模,最后利用平面向量的数量积的法则求得cosθ的值.
解答:解:设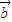 =(x,y),
=(x,y),
故2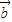 -
-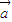 =(2x-3,2y-3)=(-1,1)?x=1,y=2,
=(2x-3,2y-3)=(-1,1)?x=1,y=2,
即b=(1,2),则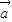 •
•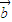 =(3,3)•(1,2)=9,|
=(3,3)•(1,2)=9,|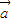 |=3
|=3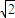 ,|b|=
,|b|= ,
,
故cosθ=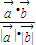 =
=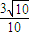
故答案为: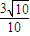
点评:本题考查平面向量的数量积的坐标运算,考查了学生对向量基础知识的应用.
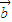 的坐标,利用2
的坐标,利用2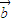 -
-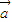 =(-1,1)求得x和y,进而求得两向量的积,和两向量的模,最后利用平面向量的数量积的法则求得cosθ的值.
=(-1,1)求得x和y,进而求得两向量的积,和两向量的模,最后利用平面向量的数量积的法则求得cosθ的值.解答:解:设
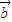 =(x,y),
=(x,y),故2
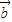 -
-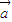 =(2x-3,2y-3)=(-1,1)?x=1,y=2,
=(2x-3,2y-3)=(-1,1)?x=1,y=2,即b=(1,2),则
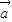 •
•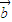 =(3,3)•(1,2)=9,|
=(3,3)•(1,2)=9,|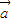 |=3
|=3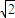 ,|b|=
,|b|= ,
,故cosθ=
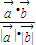 =
=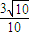
故答案为:
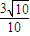
点评:本题考查平面向量的数量积的坐标运算,考查了学生对向量基础知识的应用.

练习册系列答案
相关题目
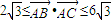 ,设
,设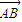 与
与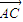 的夹角为θ.
的夹角为θ.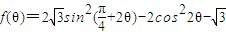 的零点.
的零点.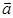 、
、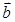 、
、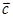 ,且满足
,且满足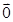 ,|
,|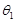 ,
,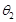 ,
,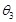 ,则它们的大小关系是( )
,则它们的大小关系是( )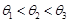 B.
B.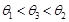
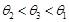 D.
D.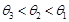
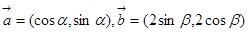 ,且
,且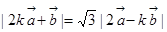 (
(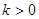 ),设
),设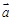 与
与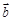 的夹角为
的夹角为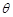
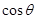 与
与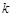 的函数关系式;
的函数关系式;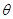 取最大值时,求
取最大值时,求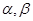 满足的关系式.
满足的关系式.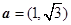 ,
,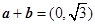 ,设
,设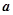 与
与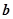 的夹角为
的夹角为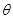 ,则
,则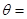 _____
_____  ,且
,且 (
( ),
), 与
与 的夹角为
的夹角为
 与
与 的函数关系式;
的函数关系式; 取最大值时,求
取最大值时,求 满足的关系式.
满足的关系式.