题目内容
如果过点(0,1)斜率为k的直线l与圆x2+y2+kx+my-4=0交于M、N两点,且M、N关于直线x+y=0对称,那么直线l的斜率k= ;不等式组 表示的平面区域的面积是 .
表示的平面区域的面积是 .
【答案】分析:根据直线l与直线x+y=0垂直,斜率之积等于-1,求出直线l的斜率,化简不等式组,结合图形求不等式组表示的平面区域的面积.
解答: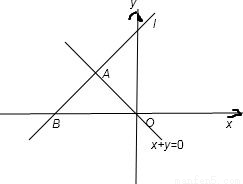 解:∵斜率为k的直线l与圆x2+y2+kx+my-4=0交于M、N两点,
解:∵斜率为k的直线l与圆x2+y2+kx+my-4=0交于M、N两点,
且M、N关于直线x+y=0对称,
∴直线l与直线x+y=0垂直,斜率之积等于-1,
∴直线l的斜率k=1.
圆方程即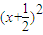 +
+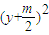 =
=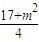 ,圆心在直线x+y=0上,
,圆心在直线x+y=0上,
∴m=-1.
不等式组即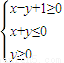 ,表示的区域如图所示△AOB,
,表示的区域如图所示△AOB,
易求A( ,
, ),B(1,0),
),B(1,0),
∴三角形AOB的面积等于 ×1×
×1× =
= ,
,
故答案为 1, .
.
点评:本题考查两条直线垂直的条件,以及求二元一次不等式组表示平面区域的面积的求法.
解答:
 解:∵斜率为k的直线l与圆x2+y2+kx+my-4=0交于M、N两点,
解:∵斜率为k的直线l与圆x2+y2+kx+my-4=0交于M、N两点,且M、N关于直线x+y=0对称,
∴直线l与直线x+y=0垂直,斜率之积等于-1,
∴直线l的斜率k=1.
圆方程即
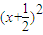 +
+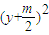 =
=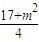 ,圆心在直线x+y=0上,
,圆心在直线x+y=0上,∴m=-1.
不等式组即
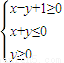 ,表示的区域如图所示△AOB,
,表示的区域如图所示△AOB,易求A(
 ,
, ),B(1,0),
),B(1,0),∴三角形AOB的面积等于
 ×1×
×1× =
= ,
,故答案为 1,
 .
.点评:本题考查两条直线垂直的条件,以及求二元一次不等式组表示平面区域的面积的求法.

练习册系列答案
相关题目
 表示的平面区域的面积是__________.
表示的平面区域的面积是__________. 表示的平面区域的面积是 .
表示的平面区域的面积是 . 表示的平面区域的面积是 .
表示的平面区域的面积是 .