题目内容
如图所示,在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.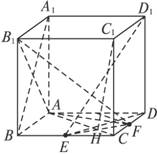
(1)试确定点F的位置,使得D1E⊥平面AB1F;
(2)当D1E⊥平面AB1F时,求二面角C1EFA的大小(结果用反三角函数值表示).
剖析:(1)先假设D1E⊥面AB1F,再用三垂线定理验证D1E⊥AF,即可得出结论.
(2)由三垂线定理作出二面角,再由解直角三角形知识求出角.
(3)本题也可用空间向量知识求解.
解法一:(1)如图,连结A1B,则A1B是D1E在面ABB1A1内的射影.

因为AB1⊥A1B,所以D1E⊥AB1.
于是D1E⊥平面AB1F![]() D1E⊥AF.
D1E⊥AF.
连结DE,则DE是D1E在底面ABCD内的射影.
因为D1E⊥AF![]() DE⊥AF,又因为ABCD是正方形,E是BC的中点,
DE⊥AF,又因为ABCD是正方形,E是BC的中点,
所以当且仅当F是CD的中点时,DE⊥AF,
即当点F是CD的中点时,D1E⊥平面AB1F.
(2)当D1E⊥平面AB1F时,由(1)知点F是CD的中点,
又已知点E是BC的中点,连结EF,则EF∥BD.
连结AC,设AC与EF交于点H,则CH⊥EF.
连结C1H,则CH是C1H在底面ABCD内的射影.
所以C1H⊥EF,即∠C1HC是二面角C1EFC的平面角.
在Rt△C1CH中,因为C1C=1,CH=![]() AC=
AC=![]() ,所以tan∠C1HC=
,所以tan∠C1HC=![]() =
=![]() =2
=2![]() .
.
所以∠C1HC=arctan2![]() ,从而∠AHC1=π-arctan2
,从而∠AHC1=π-arctan2![]() .
.
故二面角C1EFA的大小为π-arctan2![]() .
.
解法二:以A为坐标原点,建立如图所示的空间直角坐标系.
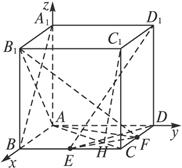
(1)设DF=x,则A(0,0,0),B(1,0,0),D(0,1,0),A1(0,0,1),B1(1,0,1),D1(0,1,1),E(1, ![]() ,0),F(x,1,0).
,0),F(x,1,0).
所以![]() =(1,-
=(1,-![]() ,-1),
,-1), ![]() =(1,0,1),
=(1,0,1), ![]() =(x,1,0).
=(x,1,0).
所以![]() ·
·![]() =1-1=0,即D1E⊥AB1.
=1-1=0,即D1E⊥AB1.
于是D1E⊥平面AB1F![]() D1E⊥AF
D1E⊥AF![]()
![]() ·
·![]() =0
=0![]() x-
x-![]() =0,即x=
=0,即x=![]() .
.
故当点F是CD的中点时,D1E⊥平面AB1F.
(2)当D1E⊥平面AB1F时,F是CD的中点.又E是BC的中点,连结EF,则EF∥BD.
连结AC,设AC与EF交于点H,则AH⊥EF.连结C1H,则CH是C1H在底面ABCD内的射影.
所以C1H⊥EF,即∠AHC1是二面角C1-EF-A的平面角.
因为C1(1,1,1)、H(![]() ,
,![]() ,0),
,0),
所以![]() =(
=(![]() ,
,![]() ,1),
,1), ![]() =(-
=(-![]() ,-
,-![]() ,0).
,0).
所以cos∠AHC1=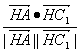 =
=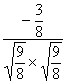 =-
=-![]() ,
,
即∠AHC1=arccos(-![]() )=π-arccos
)=π-arccos![]() .
.
故二面角C1EFA的大小为π-arccos![]() .
.
讲评:本题通过一典型图形正方体,考查了线面关系和线线关系(垂直、平行),又考查了正方体的一些性质,同时考查了学生的空间想象能力、逻辑推理能力及运算能力.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 如图所示,在棱长为1的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为
如图所示,在棱长为1的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为 一点
一点 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 最短,则
最短,则
 B.
B. C.
C. D.
D.
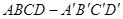 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 取得最小值,则此最小值为
取得最小值,则此最小值为 
 的面
的面 上存在一点
上存在一点 使得
使得 取得最小值,则此
取得最小值,则此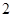 B.
B. C.
C. D.
D.