题目内容
 如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是弧TN上一点.设∠TAP=θ,长方形PQCR的面积为S平方米.
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是弧TN上一点.设∠TAP=θ,长方形PQCR的面积为S平方米.(1)求S关于θ的函数解析式;
(2)求S的最大值及此时θ的值.
分析:(1)延长RP交AB于E,延长QP交AD于F,求出PR、PQ的值,从而可得长方形PQCR的面积关于θ的函数解析式;
(2)利用换元法转化为t的函数,再利用配方法,即可求得结论.
(2)利用换元法转化为t的函数,再利用配方法,即可求得结论.
解答: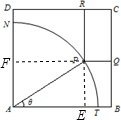 解:(1)延长RP交AB于E,延长QP交AD于F,
解:(1)延长RP交AB于E,延长QP交AD于F,
由ABCD是正方形,PRCQ是矩形,可知PE⊥AB,PF⊥AD,
由∠TAP=θ,可得EP=6cosθ,FP=6sinθ,∴PR=7-6sinθ,PQ=7-6cosθ,
∴S=PR•PQ=(7-6sinθ)(7-6cosθ)=49-42(sinθ+cosθ)+36sinθcosθ
故S关于θ的函数解析式为S=49-42(sinθ+cosθ)+36sinθcosθ(0≤θ≤
)…(4分)
(2)由sinθ+cosθ=t,可得t2=(sinθ+cosθ)2=1+2sinθcosθ,即sinθcosθ=
,
∴S=49-42t+18(t2-1)=18t2-42t+31. …(7分)
又由0≤θ≤
,可得
≤θ+
≤
,
故t=sinθ+cosθ=
sin(θ+
)∈[1,
],
∴S关于t的表达式为S=18t2-42t+31(t∈[1,
]).…(9分)
又由S=18(t-
)2+
,t∈[1,
]
可知当t=
时,S取最大值,
故S的最大值为67-42
. …(12分)
 解:(1)延长RP交AB于E,延长QP交AD于F,
解:(1)延长RP交AB于E,延长QP交AD于F,由ABCD是正方形,PRCQ是矩形,可知PE⊥AB,PF⊥AD,
由∠TAP=θ,可得EP=6cosθ,FP=6sinθ,∴PR=7-6sinθ,PQ=7-6cosθ,
∴S=PR•PQ=(7-6sinθ)(7-6cosθ)=49-42(sinθ+cosθ)+36sinθcosθ
故S关于θ的函数解析式为S=49-42(sinθ+cosθ)+36sinθcosθ(0≤θ≤
| π |
| 2 |
(2)由sinθ+cosθ=t,可得t2=(sinθ+cosθ)2=1+2sinθcosθ,即sinθcosθ=
| t2-1 |
| 2 |
∴S=49-42t+18(t2-1)=18t2-42t+31. …(7分)
又由0≤θ≤
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
故t=sinθ+cosθ=
| 2 |
| π |
| 4 |
| 2 |
∴S关于t的表达式为S=18t2-42t+31(t∈[1,
| 2 |
又由S=18(t-
| 7 |
| 6 |
| 13 |
| 2 |
| 2 |
可知当t=
| 2 |
故S的最大值为67-42
| 2 |
点评:本题考查三角函数模型的建立,考查换元法、配方法的运用,考查学生的计算能力,求得函数解析式是关键.

练习册系列答案
相关题目
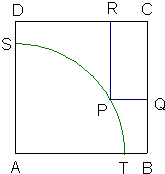 如图所示,ABCD是一块边长为100米的正方形地皮,其中ATPS是一个半径为90米的扇形小山,P是弧TS上一点,其余都是平地.现要在平地上建造矩形停车场PQCR,求停车场PQCR的最大面积.
如图所示,ABCD是一块边长为100米的正方形地皮,其中ATPS是一个半径为90米的扇形小山,P是弧TS上一点,其余都是平地.现要在平地上建造矩形停车场PQCR,求停车场PQCR的最大面积.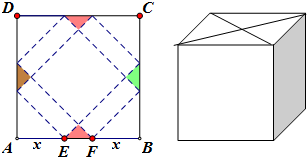 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm). 11、如图所示,ABCD是一个平面图形的斜二侧直观图,则该图形是( )
11、如图所示,ABCD是一个平面图形的斜二侧直观图,则该图形是( ) 如图所示,ABCD是一平面图形的水平放置的斜二侧直观图.在斜二侧直观图中,ABCD是一直角梯形,AB∥CD,AD⊥CD,且BC与y轴平行.若AB=6,AD=2,则这个平面图形的实际面积为( )
如图所示,ABCD是一平面图形的水平放置的斜二侧直观图.在斜二侧直观图中,ABCD是一直角梯形,AB∥CD,AD⊥CD,且BC与y轴平行.若AB=6,AD=2,则这个平面图形的实际面积为( )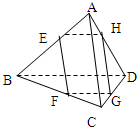 如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且AC⊥BD,AC=m,BD=n,则四 边形EFGH的面积为
如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且AC⊥BD,AC=m,BD=n,则四 边形EFGH的面积为