题目内容
(1)已知f(x-3)=x2+3x+1,求f(x)的解析式;(2)已知f(x)满足f(x-
)=x2+
,求函数f(x)的解析式;
(3)已知函数f(x)是一次函数,且f［f(x)］=4x+1,求函数f(x)的解析式.
思路解析:解决此类问题的关键是找出对应关系,找对应关系常用的方法有三种,即拼凑法、换元法、待定系数法. 解:(1)方法一:拼凑法. ∵f(x-3)=x2+3x+1=(x-3)2+6x-9+3x+1=(x-3)2+9x-8=(x-3)2+9(x-3)+27-8 =(x-3)2+9(x-3)+19, ∴f(x)=x2+9x+19. 方法二:换元法. 令t=x-3,则x=t+3, ∴f(t)=(t+3)2+3(t+3)+1=t2+9t+19. ∴f(x)=x2+9x+19. (2)设x- ∴所求函数的解析式为f(x)=x2+2. (3)设f(x)=kx+b(k≠0), ∴f［f(x)］=f(kx+b)=k(kx+b)+b=k2x+kb+b. 又∵对x∈R总有f［f(x)］=k2x+kb+b=4x+1, ∴ ∴f(x)的解析式为f(x)=2x+ 深化升华 (1)拼凑法需要较高的变形能力,通过对已有解析式进行变形,找出对应关系; (2)换元法是解决此类问题在逻辑上最容易接受的一种方法,通过换元找出对应关系; (3)待定系数法在应用时,一定要弄清函数类型,切不可盲目下手.=t,则(x-)2=t2,∴x2+
=t2+2.∴f(t)=t2+2.
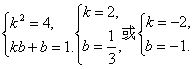
,或f(x)=-2x-1.
普通高中招生考试命题指导纲要系列答案
高分计划系列答案
高效测评单元测评系列答案
高效测评小学升学全真模拟试卷系列答案
高效复习系列答案
高效课堂小升初毕业总复习系列答案
高效期末复习系列答案
高效期末卷系列答案
高中数学知识方法和实践系列答案
学业水平测试模块强化训练系列答案