题目内容
已知函数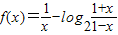 ,
,(Ⅰ)求f(x)的定义域;
(Ⅱ)判断并证明f(x)的奇偶性;
(Ⅲ)在(0,1)内,求使关系式
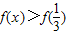 成立的实数x的取值范围.
成立的实数x的取值范围.
【答案】分析:(I)根据分式函数分母不能为零和对数函数真数大于零求解;
(Ⅱ)由(1)知定义域关于原点对称,再分析f(-x)与f(x)的关系;
(Ⅲ)先证明f(x)在(0,1)内单调递减,即在给定的区间上任取两个变量,且界定其大小,再作差变形,再与零进行比较,关键是变形到位用上条件.最后利用单调性将原不等式转化为整式不等式求解即可.
解答:解:(Ⅰ)函数f(x)有意义,需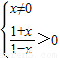
解得-1<x<1且x≠0,
∴函数定义域为x|-1<x<0或0<x<1;
(Ⅱ)函数f(x)为奇函数,
∵f(-x)=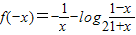 =
=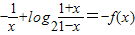 ,
,
又由(1)已知f(x)的定义域关于原点对称,
∴f(x)为奇函数;
(Ⅲ)设0<x1<x2<1,∵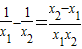 ,
,
又x1x2>0,x2-x1>0,∴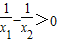 ①
①
又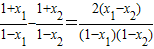 ,∵1-x1>0,1-x2>0,x1-x2<0,
,∵1-x1>0,1-x2>0,x1-x2<0,
∴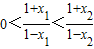 ;
;
∴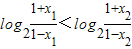 .②
.②
由①②,得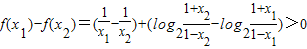 ,
,
∴f(x)在(0,1)内为减函数;
又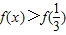 ,∴使
,∴使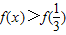 成立x的范围是
成立x的范围是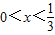 .
.
点评:本题主要考查函数的基本性质,涉及到定义域的求法,要注意分式函数,根式函数和基本函数的定义域;还考查了奇偶性的判断,要注意定义域.
(Ⅱ)由(1)知定义域关于原点对称,再分析f(-x)与f(x)的关系;
(Ⅲ)先证明f(x)在(0,1)内单调递减,即在给定的区间上任取两个变量,且界定其大小,再作差变形,再与零进行比较,关键是变形到位用上条件.最后利用单调性将原不等式转化为整式不等式求解即可.
解答:解:(Ⅰ)函数f(x)有意义,需
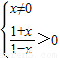
解得-1<x<1且x≠0,
∴函数定义域为x|-1<x<0或0<x<1;
(Ⅱ)函数f(x)为奇函数,
∵f(-x)=
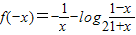 =
=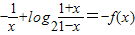 ,
,又由(1)已知f(x)的定义域关于原点对称,
∴f(x)为奇函数;
(Ⅲ)设0<x1<x2<1,∵
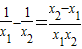 ,
,又x1x2>0,x2-x1>0,∴
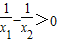 ①
①又
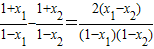 ,∵1-x1>0,1-x2>0,x1-x2<0,
,∵1-x1>0,1-x2>0,x1-x2<0,∴
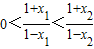 ;
;∴
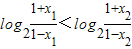 .②
.②由①②,得
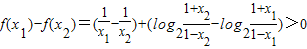 ,
,∴f(x)在(0,1)内为减函数;
又
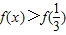 ,∴使
,∴使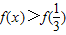 成立x的范围是
成立x的范围是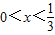 .
.点评:本题主要考查函数的基本性质,涉及到定义域的求法,要注意分式函数,根式函数和基本函数的定义域;还考查了奇偶性的判断,要注意定义域.

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.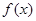 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求