题目内容
10．已知$\overrightarrow{a}$=（-1，-3，2），$\overrightarrow{b}$=（1，2，0），若存在$\overrightarrow{c}$使$\overrightarrow{a}$∥$\overrightarrow{c}$且$\overrightarrow{b}$•$\overrightarrow{c}$=5，则$\overrightarrow{c}$=（$\frac{5}{7}$，$\frac{15}{7}$，-$\frac{10}{7}$）．分析 设出向量$\overrightarrow{c}$的坐标，根据空间向量共线以及数量积的坐标表示，列出方程，求出向量$\overrightarrow{c}$．
解答 解：设$\overrightarrow{c}$=（x，y，z），
∵$\overrightarrow{a}$=（-1，-3，2），$\overrightarrow{b}$=（1，2，0），
且$\overrightarrow{a}$∥$\overrightarrow{c}$，
∴$\frac{x}{-1}$=$\frac{y}{-3}$=$\frac{z}{2}$，①
又$\overrightarrow{b}$•$\overrightarrow{c}$=5，∴x+2y=5，②
由①②解得x=$\frac{5}{7}$，y=$\frac{15}{7}$，z=-$\frac{10}{7}$；
∴$\overrightarrow{c}$=（$\frac{5}{7}$，$\frac{15}{7}$，-$\frac{10}{7}$）．
故答案为：（$\frac{5}{7}$，$\frac{15}{7}$，-$\frac{10}{7}$）．
点评 本题考查了空间向量共线以及数量积的坐标运算问题，是基础题目．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
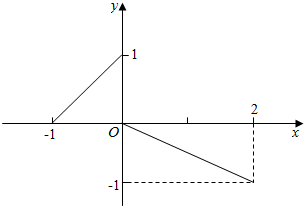
1．f（x）图象如图，则f（x）=$\left\{\begin{array}{l}{x+1}&{-1≤x≤0}\\{-\frac{1}{2}x}&{0＜x≤2}\end{array}\right.$．
1．已知单位向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为120°，且|$\overrightarrow{c}$-$\overrightarrow{a}$|+|$\overrightarrow{c}$-$\overrightarrow{b}$|=$\sqrt{3}$，则|$\overrightarrow{c}$+2$\overrightarrow{a}$|的取值范围是（ ）
| A． | [$\frac{3}{2}$，+∞） | B． | [$\sqrt{3}$，3] | C． | [$\sqrt{3}$，+∞） | D． | [$\frac{3}{2}$，3] |
5．已知圆的参数方程$\left\{\begin{array}{l}{x=2cosθ+2}\\{y=2sinθ-1}\end{array}\right.$，则该圆的圆心为（ ）
| A． | （-2，1） | B． | （2，-1） | C． | （2，1） | D． | （-2，-1） |