题目内容
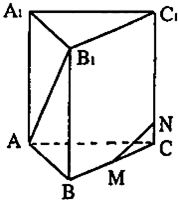 (2010•湖北模拟)如图所示,在正三棱柱ABC-A1B1C1中,BB1=BC=2,且M是BC的中点,点N在CC1上,NC=
(2010•湖北模拟)如图所示,在正三棱柱ABC-A1B1C1中,BB1=BC=2,且M是BC的中点,点N在CC1上,NC=| 1 | 2 |
(1)求证:AB1⊥MN
(2)求二面角M-AB1-N的大小.
分析:(1)可利用三垂线定理证明:即证明MN与AB1的射影垂直.故可连接MA、B1M则根据正三棱柱ABC-A1B1C1中的性质可得平面ABC⊥平面BB1C1C再利用面面垂直的性质定理可得
AM⊥平面BB1C1C从而可得B1M是AB1在平面BB1C1C上的射影然后再利用三角形的有关知识证明出B1M⊥MN即可.
(2)利用二面角的定义先将二面角M-AB1-N的平面角作出来然后在解三角形即可:由(1)知可过点M作ME⊥AB1,垂足为E,连接EN则根据三垂线定理可得EN⊥AB1则根据二面角的定义∠MEN即为二面角M-AB1-N的平面角然后在解三角形MEN求出∠MEN即可.
AM⊥平面BB1C1C从而可得B1M是AB1在平面BB1C1C上的射影然后再利用三角形的有关知识证明出B1M⊥MN即可.
(2)利用二面角的定义先将二面角M-AB1-N的平面角作出来然后在解三角形即可:由(1)知可过点M作ME⊥AB1,垂足为E,连接EN则根据三垂线定理可得EN⊥AB1则根据二面角的定义∠MEN即为二面角M-AB1-N的平面角然后在解三角形MEN求出∠MEN即可.
解答:解:(1)连接MA、B1M,
在正△ABC中AM⊥BC,
又∵平面ABC⊥平面BB1C1C,
∴AM⊥平面BB1C1C,B1M是AB1在平面BB1C1C上的射影,M是BC的中点,N在CC1上,NC=
∴在Rt△B1BM与Rt△MCN中,
=
=
,
∴∠BB1M=∠NMC,∠BMB1=∠MNC,∴∠B1MN=90°.
∴B1M⊥MN,由三垂线定理知AB1⊥MN.(6分)
(2)过点M作ME⊥AB1,垂足为E,连接EN,由(1)知MN⊥平面AMB1,
∴EN⊥AB1(三垂线定理),∴∠MEN即为二面角M-AB1-N的平面角,由AM⊥平面BC1,知AM⊥B1M.
在Rt△AMB1中,ME=
=
,又MN=
=
,
故在Rt△EMN中,tan∠MEN=
=
,
∴二面角M-AB1-N的正切值为
在正△ABC中AM⊥BC,
又∵平面ABC⊥平面BB1C1C,
∴AM⊥平面BB1C1C,B1M是AB1在平面BB1C1C上的射影,M是BC的中点,N在CC1上,NC=
| 1 |
| 2 |
∴在Rt△B1BM与Rt△MCN中,
| NC |
| MC |
| BM |
| BB1 |
| 1 |
| 2 |
∴∠BB1M=∠NMC,∠BMB1=∠MNC,∴∠B1MN=90°.
∴B1M⊥MN,由三垂线定理知AB1⊥MN.(6分)
(2)过点M作ME⊥AB1,垂足为E,连接EN,由(1)知MN⊥平面AMB1,
∴EN⊥AB1(三垂线定理),∴∠MEN即为二面角M-AB1-N的平面角,由AM⊥平面BC1,知AM⊥B1M.
在Rt△AMB1中,ME=
| ||||
2
|
| ||
| 4 |
1+(
|
| ||
| 2 |
故在Rt△EMN中,tan∠MEN=
| MN |
| ME |
| ||
| 3 |
∴二面角M-AB1-N的正切值为
| ||
| 3 |
点评:本题主要考察了线线垂直的证明和二面角的求解,属常考题目,较难.解题的关键是要掌握证明线线垂直的常用方法:三垂线定理或其逆定理而对于二面角的求解要现根据二面角的定义作出其平面角然后再证明此角即为其平面角即常说的“先作后证”!

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 (2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )
(2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( ) (2010•湖北模拟)如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(2010•湖北模拟)如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.