题目内容
设命题p：关于x 的不等式x2+2ax+4>0 对一切x ∈R 恒成立，q：函数f(x)=-(4-2a)x 在（- ∞，+ ∞）上是减函数．是否存在实数a ，使得两个命题中有且仅有一个是真命题？若存在，求出实数a 的取值范围；若不存在，请说明理由．
解：假设存在实数a 使得命题p 、q 中有且仅有一个是真命题，
不妨设集合A={a|x2+2ax+4>0 对一切x ∈R 恒成立} ，
集合B={a|f(x)=-(4-2a)x 在（- ∞，+ ∞）上是减函数} ．
由x2+2ax+4>0 ，得Δ=(2a)2-4 ×4 <0,-2<a<2,
∴A={a|-2<a<2}.
由f(x)=-(4-2a)x 在（- ∞，+ ∞）上是减函数，得4-2a>1,
即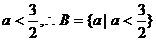
∵命题p、q中有且仅有一个是真命题，
∴命题p真且命题q假，或命题p假且命题q真．
∴问题转化为求[A∩(CUB]∪[(CUA)∩B]．
∵CRA={a|a≤-2或a≥2},CRB=
∴A∩(CRB)=
(CRA)∩B={a|a≤-2},
∴实数n的取值范围是{a|a ≤-2 或
不妨设集合A={a|x2+2ax+4>0 对一切x ∈R 恒成立} ，
集合B={a|f(x)=-(4-2a)x 在（- ∞，+ ∞）上是减函数} ．
由x2+2ax+4>0 ，得Δ=(2a)2-4 ×4 <0,-2<a<2,
∴A={a|-2<a<2}.
由f(x)=-(4-2a)x 在（- ∞，+ ∞）上是减函数，得4-2a>1,
即
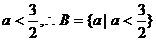
∵命题p、q中有且仅有一个是真命题，
∴命题p真且命题q假，或命题p假且命题q真．
∴问题转化为求[A∩(CUB]∪[(CUA)∩B]．
∵CRA={a|a≤-2或a≥2},CRB=
∴A∩(CRB)=
(CRA)∩B={a|a≤-2},∴实数n的取值范围是{a|a ≤-2 或
练习册系列答案
天天练口算系列答案
相关题目
设命题P：关于x的不等式a1x2+b1x+c1＞0与a2x2+b2x+c2＞0的解集相同；命题Q：
=
=
，则命题Q是命题P的（ ）
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| A、充要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、既不充分也不必要条件 |