题目内容
已知曲线S：y=2x-x3．
（1）求曲线S在点A（1，1）处的切线方程；
（2）求过点B（2，0）并与曲线S相切的直线方程．
（1）求曲线S在点A（1，1）处的切线方程；
（2）求过点B（2，0）并与曲线S相切的直线方程．
分析：（1）先对函数进行求导，根据导函数在点A处的值为切线方程的斜率可得答案．
（2）先设切点坐标，然后得出斜率的表达式求出斜率，最后根据直线的点斜式方程可得答案．
（2）先设切点坐标，然后得出斜率的表达式求出斜率，最后根据直线的点斜式方程可得答案．
解答：解：（1）∵y=2x-x3∴y'=-3x2+2
当x=1时，y'=-1
∴点A（1，1）处的切线方程为：y-1=（-1）（x-1） 即：x+y-2=0
（2）设切点坐标为（m，2m-m3）
则直线斜率k=
y'=2-3m2，整理得到：m3-3m2+2=0
m3-m2-2（m2-1）=0
m2（m-1）-2（m+1）（m-1）=0
（m-1）（m2-2m-2）=0
解得m1=1，m2=1+
，m3=1-
当m=1时：k=2-3m2=-1，直线方程为y=-（x-2）=2-x；
当m=1+
时，k=2-3m2=-10-6
，直线方程为y=（-10-6
）（x-2）
当m=1-
时，k=2-3m2=-10+6
，直线方程为y=（-10+6
）（x-2）
当x=1时，y'=-1
∴点A（1，1）处的切线方程为：y-1=（-1）（x-1） 即：x+y-2=0
（2）设切点坐标为（m，2m-m3）
则直线斜率k=
| 2m-m3 |
| m-2 |
m3-m2-2（m2-1）=0
m2（m-1）-2（m+1）（m-1）=0
（m-1）（m2-2m-2）=0
解得m1=1，m2=1+
| 3 |
| 3 |
当m=1时：k=2-3m2=-1，直线方程为y=-（x-2）=2-x；
当m=1+
| 3 |
| 3 |
| 3 |
当m=1-
| 3 |
| 3 |
| 3 |
点评：本题主要考查导数的几何意义，即函数在某点的导数值等于过该点的曲线的切线的斜率．
练习册系列答案
相关题目
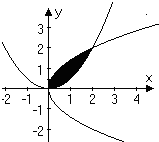已知曲线C1：y2=2x与C2：y=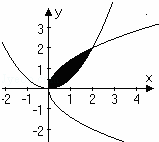
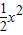在第一象限内交点为P．
在第一象限内交点为P．