题目内容
19.若m-$\frac{1}{2}<\\;x<m+\frac{1}{2}$x≤m+$\frac{1}{2}$(其中m为整数),则称m为离实数x最近的整数,记作[x],即[x]=m.设集合A={(x,y)|y=f(x)=x-[x],x∈R},B={(x,y)|y=g(x)=kx-1,x∈R},若集合A∩B的子集恰有4个,则实数k的取值范围是{k|$\frac{1}{3}$<k≤$\frac{3}{7}$}.分析 把A与B中的函数f(x)与g(x)图象画在同一个坐标系中,根据A与B交集的子集恰有4个,得到交集中元素有2个,利用图象求出k的范围即可.
解答 解:把f(x)=x-[x]与g(x)=kx-1图象画在同一个坐标系中,如图所示,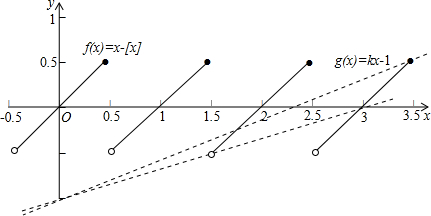
若集合A与B交集的子集有4个,即A∩B中有2个元素,
把(1.5,-0.5)代入得:k=$\frac{1}{3}$,把(3.5,0.5)代入得:k=$\frac{3}{7}$,
则k的取值范围为{k|$\frac{1}{3}$<k≤$\frac{3}{7}$}.
故答案为:{k|$\frac{1}{3}$<k≤$\frac{3}{7}$}
点评 此题考查了交集及其运算,利用了数形结合的思想,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
10.抛物线y2=4x图象上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线焦点为F,则△MPF的周长为( )
| A. | 5+$\sqrt{5}$ | B. | 5+2$\sqrt{5}$ | C. | 10 | D. | 10+2$\sqrt{5}$ |
7.抛物线x2=-8y的焦点坐标是( )
| A. | (0,2) | B. | (0,-2) | C. | (0,4) | D. | (0,-4) |
4. 某四面体的三视图如图所示,且四个顶点都在一个球面上,则球面的表面积为( )
某四面体的三视图如图所示,且四个顶点都在一个球面上,则球面的表面积为( )
 某四面体的三视图如图所示,且四个顶点都在一个球面上,则球面的表面积为( )
某四面体的三视图如图所示,且四个顶点都在一个球面上,则球面的表面积为( )| A. | $\frac{11π}{3}$ | B. | 5π | C. | 7π | D. | $\frac{13π}{3}$ |
11.已知m,n为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( )
| A. | α∥β,m?α,n?β⇒m∥n | B. | m⊥α,m⊥n⇒n∥α | ||
| C. | α∩β=m,n∥α,n∥β⇒n∥m | D. | m?α,n?α,m∥β,n∥β⇒α∥β |
 如图所示的是根据输入的x值计算y的值的程序框图,若x依次取数列$\left\{{\frac{{{n^2}+5}}{n}}\right\}(n∈{{N}^*})$中的项,则所得y值的最小值为( )
如图所示的是根据输入的x值计算y的值的程序框图,若x依次取数列$\left\{{\frac{{{n^2}+5}}{n}}\right\}(n∈{{N}^*})$中的项,则所得y值的最小值为( )