题目内容
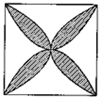如图是边长为2的正方形，以正方形中心为顶点，且分别过正方形的相邻两顶点的四条抛物线围成了图中阴影区域，随机地向正方形内投入一点，则该点落入阴影区域的概率为________．
分析：由题意知本题是一个几何概型，试验发生包含的所有事件是矩形面积，而满足条件的阴影区域，可以通过空白区域面得到，空白区域可以看作是由8部分组成，每一部分是由抛物线y=x2在[0，1]上与x轴所围成的图形的面积得到．
解答：
解：由题意知本题是一个几何概型，设正方形ABCD的边长为：2，∵试验发生包含的所有事件是矩形面积S=2×2=4，
空白区域的面积是图1中阴影部分面积的8倍，即：
8×∫01x2dx=8×
=
，∴由几何概型公式得到P=
，故答案为：
．点评：本题考查几何概型的概率，且把几何概型同几何图形的面积结合起来，几何概型和古典概型是高中必修中学习的，高考时常以选择和填空出现，有时文科会考这种类型的解答．
练习册系列答案
相关题目
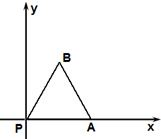如图放置的边长为1的正三角形PAB沿x轴滚动，设顶点A（x，y）的纵坐标与横坐标的函数关系式是y=f（x），则f（x）在区间[-2，1]上的解析式是
（2011•洛阳一模）如图放置的边长为1的正三角形ABC沿x轴的正方向滚动，设顶点A（x，y）的纵坐标与横坐标的函数关系是y=f（x）．则f（x）在两个相邻零点间的图象与x轴围成的面积是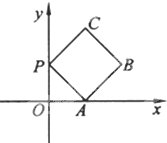
如图放置的边长为2的正方形PABC沿x轴滚动．设顶点P（x，y）的纵坐标与横坐标的函数关系是y=f（x），则f（x）的最小正周期为
