题目内容
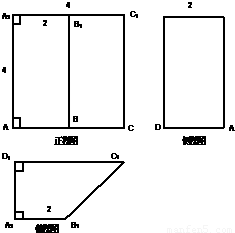
 已知:右图为一个多面体ABCD-A1B1C1D1的三视图,其中各边长度及位置关系如三视图所表示,
已知:右图为一个多面体ABCD-A1B1C1D1的三视图,其中各边长度及位置关系如三视图所表示,(1)求:二面角A1-DC1-B的余弦值
(2)已知点E为面对角线B1D1上的动点(不包括端点),求证:三棱锥D-EBC1的体积为定值,并求出这个定值
(注:答题时在答题卡的20题答题区域用尺、笔画出所用立体图形,标清字母,黑色笔描出)
分析:(1)根据三视图,可得直观图,建系设坐标以D点为原点,DA为OX轴,DC为OY轴,DD1为OZ轴,,可求面A1DC1,DC1B的法向量坐标,从而可求二面角A1-DC1-B的余弦值;
(2)设C1到平面BD1的距离为h,则可知h=2
,利用等体积可求三棱锥D-EBC1的体积,从而可得结论
(2)设C1到平面BD1的距离为h,则可知h=2
| 2 |
解答: 解:(1)如图,建系设坐标以D点为原点,DA为OX轴,DC为OY轴,DD1为OZ轴,则A1(2,0,4),C1(0,4,4),B(2,2,0),D(0,0,0)
解:(1)如图,建系设坐标以D点为原点,DA为OX轴,DC为OY轴,DD1为OZ轴,则A1(2,0,4),C1(0,4,4),B(2,2,0),D(0,0,0)
∴
=(2,0,4),
=(0,4,4)
设面A1DC1的法向量坐标为
=(x,y,z)
∴
,∴
,∴
=(-2,-1,1),
同理可得面DC1B的法向量坐标
=(-1,1-1)
∴二面角A1-DC1-B的余弦值为cos<
,
>= 0
(2)设C1到平面BD1的距离为h,则可知h=2
∵S△DEB=4
∴VC1-DEB=
×4
×2
=
∵VD-EBC1=VC1-DEB
∴VD-EBC1=
.为定值.
 解:(1)如图,建系设坐标以D点为原点,DA为OX轴,DC为OY轴,DD1为OZ轴,则A1(2,0,4),C1(0,4,4),B(2,2,0),D(0,0,0)
解:(1)如图,建系设坐标以D点为原点,DA为OX轴,DC为OY轴,DD1为OZ轴,则A1(2,0,4),C1(0,4,4),B(2,2,0),D(0,0,0)∴
| DA1 |
| DC1 |
设面A1DC1的法向量坐标为
| n |
∴
|
|
| n1 |
同理可得面DC1B的法向量坐标
| n2 |
∴二面角A1-DC1-B的余弦值为cos<
| n1 |
| n2 |
(2)设C1到平面BD1的距离为h,则可知h=2
| 2 |
∵S△DEB=4
| 2 |
∴VC1-DEB=
| 1 |
| 2 |
| 2 |
| 2 |
| 16 |
| 3 |
∵VD-EBC1=VC1-DEB
∴VD-EBC1=
| 16 |
| 3 |
点评:本题以三视图为载体,考查面面角,考查三棱锥的体积,关键是利用等体积转化.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
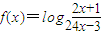 的图象是一个中心对称图形,则f(x)图象的对称中心坐标为 .
的图象是一个中心对称图形,则f(x)图象的对称中心坐标为 .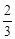 ,三个开关的闭合是相互独立的,则电路中灯亮的概率为
,三个开关的闭合是相互独立的,则电路中灯亮的概率为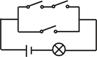
 (B)
(B) (C)
(C) (D)
(D)
 已知:右图为一个多面体ABCD-A1B1C1D1的三视图,其中各边长度及位置关系如三视图所表示,
已知:右图为一个多面体ABCD-A1B1C1D1的三视图,其中各边长度及位置关系如三视图所表示,