题目内容
某公司全年的纯利润为b元,其中一部分作为奖金发给n位职工,奖金分配方案如下:首先将职工按工作业绩(工作业绩均不相同)从大到小,由1到n排序,第1位职工得奖金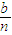 元,然后将余额除以n发给第2位职工,按此方案将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后将余额除以n发给第2位职工,按此方案将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.(1)设ak(1≤k≤n)为第k位职工所得奖金额,试求a2、a3,并用k、n和b表示ak(不必证明);
(2)证明:ak>ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义;
(3)发展基金与n和b有关,记为Pn(b).对常数b,当n变化时,求
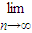 Pn(b)(可用公式
Pn(b)(可用公式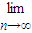 (1-
(1-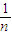 )n=
)n=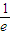 ).
).
【答案】分析:(1)根据题意可知a1进而利用余额除以n发给第2位职工,求得a2=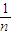 (1-
(1-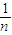 )•b,同理可求得a3.以此类推发现数列成等比数列,公比为1-
)•b,同理可求得a3.以此类推发现数列成等比数列,公比为1-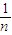 ,进求得ak.
,进求得ak.
(2)根据(1)中的ak进而代入ak-ak+1结果大于0,由题意可知业绩大的在数列的前面,且拿的奖金多,进而可判断出此奖金分配方案体现了按劳分配的原则.
(3)根据题意可分别表示出f1(b),f2(b),推断出fk(b),进而利用极限的基本运算求得 Pn(b).
Pn(b).
解答:(1)解:a1=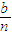 ,a2=
,a2=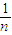 (1-
(1-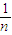 )•b,a3=
)•b,a3=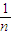 (1-
(1-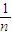 )2•b,…,ak=
)2•b,…,ak=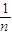 (1-
(1-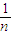 )k-1•b.
)k-1•b.
(2)证明:ak-ak+1= (1-
(1-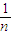 )k-1•b>0,此奖金分配方案体现了按劳分配的原则.
)k-1•b>0,此奖金分配方案体现了按劳分配的原则.
(3)解:设fk(b)表示发给第k位职工后所剩余额,
则f1(b)=(1-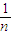 )•b,f2(b)=(1-
)•b,f2(b)=(1-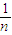 )2•b,…,fk(b)=(1-
)2•b,…,fk(b)=(1-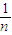 )k•b,
)k•b,
得Pn(b)=fn(b)=(1-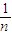 )n•b,
)n•b,
故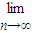 Pn(b)=
Pn(b)=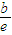 .
.
点评:本题主要考查了数列的递推式和数列的应用.考查了学生运用所学知识解决实际问题的能力.
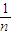 (1-
(1-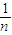 )•b,同理可求得a3.以此类推发现数列成等比数列,公比为1-
)•b,同理可求得a3.以此类推发现数列成等比数列,公比为1-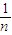 ,进求得ak.
,进求得ak.(2)根据(1)中的ak进而代入ak-ak+1结果大于0,由题意可知业绩大的在数列的前面,且拿的奖金多,进而可判断出此奖金分配方案体现了按劳分配的原则.
(3)根据题意可分别表示出f1(b),f2(b),推断出fk(b),进而利用极限的基本运算求得
 Pn(b).
Pn(b).解答:(1)解:a1=
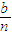 ,a2=
,a2=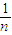 (1-
(1-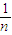 )•b,a3=
)•b,a3=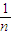 (1-
(1-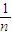 )2•b,…,ak=
)2•b,…,ak=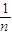 (1-
(1-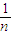 )k-1•b.
)k-1•b.(2)证明:ak-ak+1=
 (1-
(1-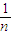 )k-1•b>0,此奖金分配方案体现了按劳分配的原则.
)k-1•b>0,此奖金分配方案体现了按劳分配的原则.(3)解:设fk(b)表示发给第k位职工后所剩余额,
则f1(b)=(1-
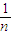 )•b,f2(b)=(1-
)•b,f2(b)=(1-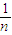 )2•b,…,fk(b)=(1-
)2•b,…,fk(b)=(1-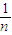 )k•b,
)k•b,得Pn(b)=fn(b)=(1-
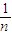 )n•b,
)n•b,故
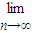 Pn(b)=
Pn(b)=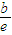 .
.点评:本题主要考查了数列的递推式和数列的应用.考查了学生运用所学知识解决实际问题的能力.

练习册系列答案
相关题目