题目内容
19.已知抛物线y2=4x的焦点为F,A、B是抛物线上两动点,且$\overrightarrow{AF}$=λ$\overrightarrow{FB}$(λ>0).(1)求证:△ABO为钝角三角形;
(2)若λ∈[4,9],求△ABO面积的取值范围.
分析 (1)设直线l的方程为my=x-1,联立直线与抛物线,利用韦达定理,证明$\overrightarrow{OA}$•$\overrightarrow{OB}$<0,即可证明:△ABO为钝角三角形;
(2)S△AOB=$\frac{1}{2}$|OF||y1-y2|=2$\sqrt{1+{m}^{2}}$,$\overrightarrow{AF}$=λ$\overrightarrow{FB}$,可得y1=-λy2,代入①可得m2=$\frac{(1-λ)^{2}}{4λ}$=$\frac{1}{4}$(λ+$\frac{1}{λ}$)-$\frac{1}{2}$,利用λ∈[4,9],即可求△ABO面积的取值范围.
解答 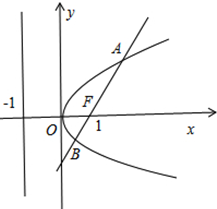 (1)证明:抛物线C的方程为y2=4x,F(1,0)
(1)证明:抛物线C的方程为y2=4x,F(1,0)
设A(x1,y1),B(x2,y2).
设直线l的方程为my=x-1,联立直线与抛物线,
消去x得到y2-4my-4=0,∴y1+y2=4m,y1y2=-4①.
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=(my1+1)(my2+1)+y1y2=(m2+1)y1y2+m(y1+y2)+1=-4(m2+1)+4m2+1=-3<0,
∴△ABO为钝角三角形;
(2)解:由(1)可知:|y1-y2|=4$\sqrt{1+{m}^{2}}$.
∴S△AOB=$\frac{1}{2}$|OF||y1-y2|=2$\sqrt{1+{m}^{2}}$,
∵$\overrightarrow{AF}$=λ$\overrightarrow{FB}$,
∴(1-x1,-y1)=λ(x2-1,y2).
∴y1=-λy2,
代入①可得m2=$\frac{(1-λ)^{2}}{4λ}$=$\frac{1}{4}$(λ+$\frac{1}{λ}$)-$\frac{1}{2}$,
∵λ∈[4,9],∴λ+$\frac{1}{λ}$在[4,9]上单调递增,∴λ+$\frac{1}{λ}$∈[$\frac{17}{4}$,$\frac{82}{9}$],
∴m2∈[$\frac{9}{16}$,$\frac{64}{36}$]
∴S△AOB∈[$\frac{5}{2}$,$\frac{10}{3}$].
点评 本题考查直线与抛物线的位置关系,考查三角形面积的计算,考查向量知识的运用,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\overrightarrow{AB}$+($\overrightarrow{PA}$+$\overrightarrow{BQ}$) | B. | ($\overrightarrow{AB}$+$\overrightarrow{PC}$)+($\overrightarrow{BA}$-$\overrightarrow{QC}$) | C. | $\overrightarrow{QC}$-$\overrightarrow{QP}$+$\overrightarrow{CQ}$ | D. | $\overrightarrow{PA}$+$\overrightarrow{AB}$-$\overrightarrow{BQ}$ |