题目内容
把实数a,b,c,d排形成如
|
|
|
|
|
|
|
分析:由于(ax+by,cx+dy)=(0×2+1×3,1×2+0×3)=(3,2),设(x,y)是曲线x2+4xy+2y2=1的点,在矩阵
的作用下的点为(x′,y′),得出关于a,b的方程组,从而解决问题.
|
解答:解:(ax+by,cx+dy)=(0×2+1×3,1×2+0×3)=(3,2),
设(x,y)是曲线x2+4xy+2y2=1的点,在矩阵
的作用下的点为(x′,y′),
即
又x′2-2y′2=1,∴(x+ay)2-2(bx+y)2=1,(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1.
故
?
∴a+b=2.
故答案为:2.
设(x,y)是曲线x2+4xy+2y2=1的点,在矩阵
|
即
|
故
|
|
故答案为:2.
点评:本小题主要考查几种特殊的矩阵变换、曲线与方程等基础知识,考查运算求解能力,解答的关键是利用待定系数法求解a,b;属于基础题.

练习册系列答案
相关题目
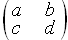 的形式,称为二行二列矩阵,定义矩阵的一种运算
的形式,称为二行二列矩阵,定义矩阵的一种运算 ,设运算的几何意义为平面直角坐标系下的点(x,y)在矩阵
,设运算的几何意义为平面直角坐标系下的点(x,y)在矩阵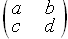 的作用下变换为点(ax+by,cx+dy),给出下列命题:
的作用下变换为点(ax+by,cx+dy),给出下列命题: