题目内容
正四棱锥的一个对角面的面积是一个侧面面积的
| ||
| 2 |
分析:设正四棱锥S-ABCD的底面边长为a,高为h,用a,h表示出对角面的面积、侧面面积,作出侧面与底面所成锐二面角的平面角,求解即可.
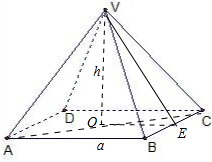
解答:解:设正四棱锥V-ABCD的底面边长为a,高为VO=h,斜高为VE,如图,∠VEO为侧面与底面所成锐二面角的平面角.
对角面S△VAC=
×AC×VO=
×
a×h=
ah
侧面 S△VBC=
BC×VE=
×a×
,
若对角面的面积是侧面面积的
倍 则得
=
化简整理得h=
a,
tanVEO=
=
,
∴∠VEO=
故答案为:

对角面S△VAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
侧面 S△VBC=
| 1 |
| 2 |
| 1 |
| 2 |
h2+
|
若对角面的面积是侧面面积的
| ||
| 2 |
| ||||
|
| ||
| 2 |
化简整理得h=
| ||
| 2 |
tanVEO=
| h | ||
|
| 3 |
∴∠VEO=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查正四棱锥的定义、性质,空间角的求解,考查了空间想象能力、计算能力,分析解决问题能力

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目


 倍,则侧面与底面所成锐二面角等于 .
倍,则侧面与底面所成锐二面角等于 .