题目内容
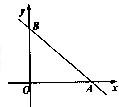 如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.
如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.
(1)求直线lAB斜率的大小;
(2)若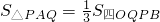 时,请你确定P点在AB上的位置,并求出线段PQ的长;
时,请你确定P点在AB上的位置,并求出线段PQ的长;
(3)在y轴上是否存在点M,使△MPQ为等腰直角三角形,若存在,求出点M的坐标;
若不存在,说明理由.
解:(1)由

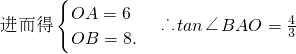 .∴k=tan∠BAO=
.∴k=tan∠BAO= .
.
(2)∵
即P为AB的中点,∴PQ=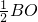 =4.
=4.
(3)由已知得l方程为4x+3y=24(*)
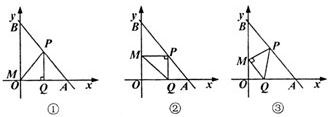
①当∠PQM=90°时,由PQ∥OB且|PQ|=|MQ|此时M点与原点O重合,设Q(a,0)则P(a,a)
有(a,a)代入(*)得a= .
. .
.
②当∠MPQ=90°,
由PQ∥OB且|MP|=|PQ|设Q(a,0)则M(0,a),P(a,a)进而得a= .
.
③当∠PMQ=90°,由PQ∥OB,|PM|=|MQ|且|OM|=|OQ|=|PQ|
设Q(a,0)则M(0,a)点P坐标为(a,2a)代入(*)得a= .
.
综上所述,y轴上有三个点M1(0,0),M2(0, )和M3(0,
)和M3(0, )满足使△PMQ为等腰直角三角形.
)满足使△PMQ为等腰直角三角形.
分析:(1)由 ,进而得到OA=6,OB=8,由此能得到直线lAB斜率的大小.
,进而得到OA=6,OB=8,由此能得到直线lAB斜率的大小.
(2)由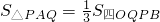 ,知
,知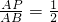 ,即P为AB的中点,由此能求出PQ=
,即P为AB的中点,由此能求出PQ=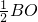 =4.
=4.
(3)由已知得l方程为4x+3y=24,然后分∠PQM=90°,∠MPQ=90°,∠PMQ=90°三种情况分别讨论,求出点M的坐标.
点评:本题考查直线和圆的位置关系,解题时要认真审题,注意分类讨论法的合理运用.

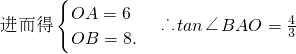 .∴k=tan∠BAO=
.∴k=tan∠BAO= .
.(2)∵

即P为AB的中点,∴PQ=
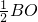 =4.
=4.(3)由已知得l方程为4x+3y=24(*)

①当∠PQM=90°时,由PQ∥OB且|PQ|=|MQ|此时M点与原点O重合,设Q(a,0)则P(a,a)
有(a,a)代入(*)得a=
 .
. .
.②当∠MPQ=90°,
由PQ∥OB且|MP|=|PQ|设Q(a,0)则M(0,a),P(a,a)进而得a=
 .
.③当∠PMQ=90°,由PQ∥OB,|PM|=|MQ|且|OM|=|OQ|=|PQ|
设Q(a,0)则M(0,a)点P坐标为(a,2a)代入(*)得a=
 .
.综上所述,y轴上有三个点M1(0,0),M2(0,
 )和M3(0,
)和M3(0, )满足使△PMQ为等腰直角三角形.
)满足使△PMQ为等腰直角三角形.分析:(1)由
 ,进而得到OA=6,OB=8,由此能得到直线lAB斜率的大小.
,进而得到OA=6,OB=8,由此能得到直线lAB斜率的大小.(2)由
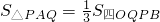 ,知
,知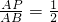 ,即P为AB的中点,由此能求出PQ=
,即P为AB的中点,由此能求出PQ=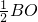 =4.
=4.(3)由已知得l方程为4x+3y=24,然后分∠PQM=90°,∠MPQ=90°,∠PMQ=90°三种情况分别讨论,求出点M的坐标.
点评:本题考查直线和圆的位置关系,解题时要认真审题,注意分类讨论法的合理运用.

练习册系列答案
相关题目
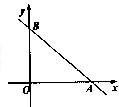 如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.
如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q. 如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点.且PQ∥OA交OB于点Q.
如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点.且PQ∥OA交OB于点Q.
