题目内容
下面给出四个命题:(1)对于实数m和向量 、
、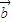 恒有:m(
恒有:m(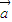 -
-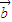 )=m
)=m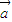 -m
-m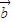 ;(2)对于实数m,n和向量
;(2)对于实数m,n和向量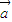 ,恒有:(m-n)
,恒有:(m-n)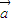 =m
=m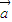 -n
-n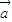 ;(3)若m
;(3)若m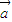 =m
=m (m∈R,m≠0),则
(m∈R,m≠0),则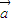 =
=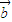 ;(4)若m
;(4)若m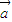 =n
=n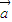 (m,n∈R),则m=n,其中正确命题的个数是( )
(m,n∈R),则m=n,其中正确命题的个数是( )A.1
B.2
C.3
D.4
【答案】分析:(1)对于实数m和向量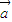 、
、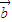 ,根据向量的数乘满足分配律,故恒有:m(
,根据向量的数乘满足分配律,故恒有:m( -
- )=m
)=m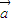 -m
-m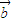 .
.
(2)对于实数m,n和向量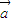 ,根据向量的数乘运算律,恒有(m-n)
,根据向量的数乘运算律,恒有(m-n)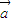 =m
=m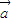 -n
-n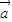 .
.
(3)若m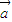 =m
=m (m∈R,m≠0),两边同时除以m,则可得
(m∈R,m≠0),两边同时除以m,则可得 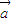 =
=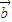 .
.
(4)若m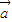 =n
=n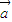 (m,n∈R),则m=n不成立,如当
(m,n∈R),则m=n不成立,如当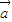 =
=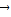 时,m和n不一定相等.
时,m和n不一定相等.
解答:解:(1)对于实数m和向量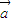 、
、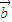 ,根据向量的数乘满足分配律,故恒有:m(
,根据向量的数乘满足分配律,故恒有:m(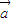 -
-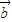 )=m
)=m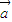 -m
-m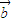 ,故(1)正确.
,故(1)正确.
(2)对于实数m,n和向量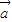 ,根据向量的数乘运算律,恒有(m-n)
,根据向量的数乘运算律,恒有(m-n)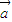 =m
=m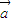 -n
-n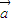 ,故 (2)正确.
,故 (2)正确.
(3)若m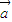 =m
=m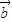 (m∈R,m≠0),两边同时除以m,则可得
(m∈R,m≠0),两边同时除以m,则可得 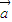 =
=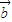 ,故(4)不正确.
,故(4)不正确.
(4)若m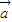 =n
=n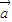 (m,n∈R),则m=n不成立,如当
(m,n∈R),则m=n不成立,如当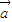 =
=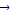 时,m和n不一定相等.
时,m和n不一定相等.
综上,(1)、(2)、(3)正确,(4)不正确,
故选 C.
点评:本题考查相等的向量,相反的向量的定义,向量的数乘法则以及其几何意义,注意考虑零向量的情况.
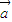 、
、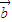 ,根据向量的数乘满足分配律,故恒有:m(
,根据向量的数乘满足分配律,故恒有:m( -
- )=m
)=m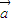 -m
-m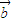 .
.(2)对于实数m,n和向量
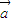 ,根据向量的数乘运算律,恒有(m-n)
,根据向量的数乘运算律,恒有(m-n)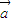 =m
=m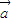 -n
-n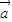 .
.(3)若m
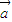 =m
=m (m∈R,m≠0),两边同时除以m,则可得
(m∈R,m≠0),两边同时除以m,则可得 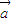 =
=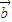 .
.(4)若m
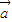 =n
=n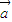 (m,n∈R),则m=n不成立,如当
(m,n∈R),则m=n不成立,如当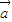 =
=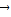 时,m和n不一定相等.
时,m和n不一定相等.解答:解:(1)对于实数m和向量
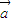 、
、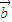 ,根据向量的数乘满足分配律,故恒有:m(
,根据向量的数乘满足分配律,故恒有:m(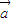 -
-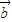 )=m
)=m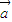 -m
-m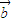 ,故(1)正确.
,故(1)正确.(2)对于实数m,n和向量
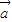 ,根据向量的数乘运算律,恒有(m-n)
,根据向量的数乘运算律,恒有(m-n)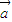 =m
=m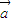 -n
-n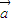 ,故 (2)正确.
,故 (2)正确.(3)若m
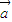 =m
=m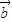 (m∈R,m≠0),两边同时除以m,则可得
(m∈R,m≠0),两边同时除以m,则可得 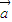 =
=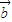 ,故(4)不正确.
,故(4)不正确.(4)若m
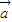 =n
=n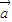 (m,n∈R),则m=n不成立,如当
(m,n∈R),则m=n不成立,如当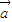 =
=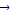 时,m和n不一定相等.
时,m和n不一定相等.综上,(1)、(2)、(3)正确,(4)不正确,
故选 C.
点评:本题考查相等的向量,相反的向量的定义,向量的数乘法则以及其几何意义,注意考虑零向量的情况.

练习册系列答案
相关题目