题目内容
已知函数f(x)=(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<![]() .
.
解:(1)将x1=3,x2=4分别代入方程![]() -x+12=0,
-x+12=0,
得
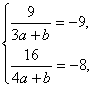 解得
解得![]()
所以f(x)=![]() (x≠2).
(x≠2).
(2)不等式即为![]() <
<![]() ,
,
可化为![]() <0,即(x-2)(x-1)(x-k)>0.
<0,即(x-2)(x-1)(x-k)>0.
①当1<k<2时,解集为x∈(1,k)∪(2,+∞);
②当k=2时,不等式为(x-2)2(x-1)>0,解集为x∈(1,2)∪(2,+∞);
③当k>2时,解集为x∈(1,2)∪(k,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|