题目内容
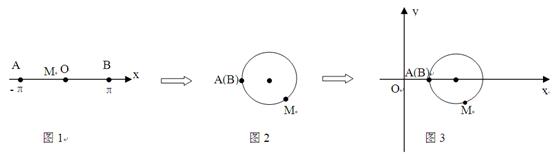
下图展示了一个由区间(―π,π)到实数集R的映射过程:区间(―π,π)中的实数x对应轴上的点M(如图1):将线段AB围成一个圆,使两端点A、B恰好重合(从A到B是逆时针,如图2):再将这个圆放在平面直角坐标系中,使其圆心在x轴上,点A的坐标为(1,0)(如图3),图3中直线OM的斜率为k,则x的象就是k,记作k=¦(x).有下列判断(1)¦(x)是奇函数;(2) ¦(x)是存在3个极值点的函数;(3) ¦(x)的值域是[―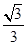 ,
,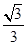 ];
];
(4) ¦(x)是区间(―π,π)上的增函数。其中正确的是
A、(1)(2) B、(1)(3) C、(2)(3) D、(1)(4)
【答案】
B
【解析】由题意(1)是正确命题,因为定义域为(―π,π)关于原点对称,根据圆的对称性易知圆上的点与原点O连线的斜率也关于原点对称,即函数k=¦(x)为奇函数;(2)由图3可以看出,x由―π增大到π时,M由A运动到B,此时直线OM的斜率为k先减小后增加然后再减小,故函数有2个极值点,即(2)错;(3)对于(3):直线OM方程为y=kx,利用圆心(2,0)到直线OM的距离等于半径j解得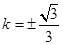 ,所以k的取值范围即函数f(x)的值域为[―
,所以k的取值范围即函数f(x)的值域为[―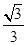 ,
,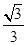 ].故(3)正确.(4)是错误命题,由图3可以看出,x由―π增大到π时,M由A运动到B,此时直线OM的斜率为k先减小后增加然后再减小,故f(x)是区间(―π,π)上的增函数是错误的;综上知(1)(3)是正确命题,故选B
].故(3)正确.(4)是错误命题,由图3可以看出,x由―π增大到π时,M由A运动到B,此时直线OM的斜率为k先减小后增加然后再减小,故f(x)是区间(―π,π)上的增函数是错误的;综上知(1)(3)是正确命题,故选B

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
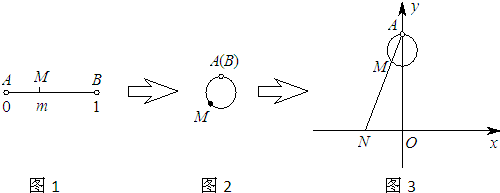
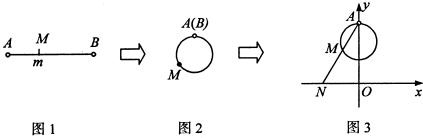
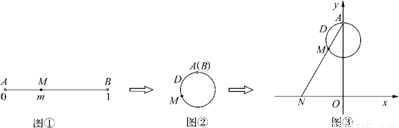
 下图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图1),将线段AB围成一个正方形,使两端点A,B恰好重合(如图2),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图3),若图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.
下图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图1),将线段AB围成一个正方形,使两端点A,B恰好重合(如图2),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图3),若图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.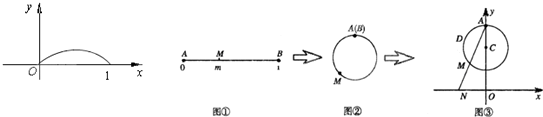
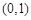 到实数集R的映射过程:区间
到实数集R的映射过程:区间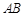 围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为
围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为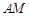 与x轴交于点
与x轴交于点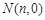 ,则m的象就是n,记作
,则m的象就是n,记作 .
.
 ;②
;②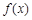 是偶函数;③
是偶函数;③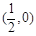 对称,则所有真命题的序号是_______.(填出所有真命题的序号)
对称,则所有真命题的序号是_______.(填出所有真命题的序号)