题目内容
已知x、y是正变数,a、b是正常数,且 =1,x+y的最小值为 .
=1,x+y的最小值为 .
【答案】分析:根据 =1,可假设
=1,可假设 =cos2θ,
=cos2θ, =sin2θ,则x=asec2θ,y=bcsc2θ,,从而将x+y转化为a+b+atan2θ+bcot2θ,进而可利用基本不等式,求出最小值.
=sin2θ,则x=asec2θ,y=bcsc2θ,,从而将x+y转化为a+b+atan2θ+bcot2θ,进而可利用基本不等式,求出最小值.
解答:解:令 =cos2θ,
=cos2θ, =sin2θ,则x=asec2θ,y=bcsc2θ,
=sin2θ,则x=asec2θ,y=bcsc2θ,
∴x+y=asec2θ+bcsc2θ=a+b+atan2θ+bcot2θ≥a+b+2 .
.
故答案为:a+b+2
点评:本题以等式为载体,考查基本不等式的运用,解题的关键是三角换元.
 =1,可假设
=1,可假设 =cos2θ,
=cos2θ, =sin2θ,则x=asec2θ,y=bcsc2θ,,从而将x+y转化为a+b+atan2θ+bcot2θ,进而可利用基本不等式,求出最小值.
=sin2θ,则x=asec2θ,y=bcsc2θ,,从而将x+y转化为a+b+atan2θ+bcot2θ,进而可利用基本不等式,求出最小值.解答:解:令
 =cos2θ,
=cos2θ, =sin2θ,则x=asec2θ,y=bcsc2θ,
=sin2θ,则x=asec2θ,y=bcsc2θ,∴x+y=asec2θ+bcsc2θ=a+b+atan2θ+bcot2θ≥a+b+2
 .
.故答案为:a+b+2

点评:本题以等式为载体,考查基本不等式的运用,解题的关键是三角换元.

练习册系列答案
相关题目
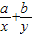 =1,x+y的最小值为 .
=1,x+y的最小值为 .