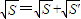题目内容
如果棱台的两底面积分别是S、S'，中截面（过棱台高的中点且平行于底面的截面）的面积是S0求证：2| S0 |
| S |
| S′ |
分析：根据棱台的两底面与中截面是相似的，设出上底和下底的边长，表示出中截面的边长，根据相似多边形的面积之比等于边长比的平方，表示出边长，得到结果．
解答：证明：设上底和下底的边长分别是a，b，
根据在侧面上三条边组成梯形的上底，下底和中位线，
得到梯形的中位线长度是
，
∵棱台的两底面与中截面是相似的，
∴三个面积之比等于边长之比的平方，
即s′=λa2，①
s=λb2，②
s0=λ(
)2③
把三个式子两边开方，
a+b=
+
，
=
，
∴2
=
+
．
根据在侧面上三条边组成梯形的上底，下底和中位线，
得到梯形的中位线长度是
| a+b |
| 2 |
∵棱台的两底面与中截面是相似的，
∴三个面积之比等于边长之比的平方，
即s′=λa2，①
s=λb2，②
s0=λ(
| a+b |
| 2 |
把三个式子两边开方，
a+b=
| s′ |
| s |
| a+b |
| 2 |
| s0 |
∴2
| S0 |
| S |
| S′ |
点评：本题考查棱台的结构特征，考查相似多边形的面积之比等于相似比的平方，考查等量代换，是一个比较简单的综合题目，这种题目可以出现在解答题目的某一问中．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
如果棱台的两底面积分别是S，S′，中截面的面积是S0，那么（ ）
A、2
| ||||||
B、S0=
| ||||||
| C、2S0=S+S′ | ||||||
| D、S02=2S'S |
．
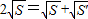