题目内容
(14分)
已知定义在 上的函数
上的函数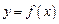 是偶函数,且
是偶函数,且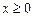 时,
时,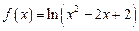 ,
,
(1)当 时,求
时,求 解析式;
解析式;
(2)写出 的单调递增区间。
的单调递增区间。
解:(1) 时,
时,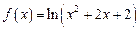 ………7分
………7分
(2)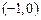 和
和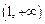 …………14分 (要有详细解答过程)
…………14分 (要有详细解答过程)
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
(14分)
已知定义在 上的函数
上的函数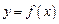 是偶函数,且
是偶函数,且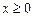 时,
时,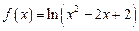 ,
,
(1)当 时,求
时,求 解析式;
解析式;
(2)写出 的单调递增区间。
的单调递增区间。
解:(1) 时,
时,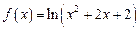 ………7分
………7分
(2)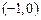 和
和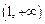 …………14分 (要有详细解答过程)
…………14分 (要有详细解答过程)
解析

 阅读快车系列答案
阅读快车系列答案