题目内容
设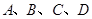 是半径为
是半径为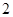 的球面上的四个不同点,且满足
的球面上的四个不同点,且满足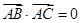 ,
,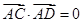 ,
,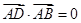 ,用
,用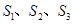 分别表示△
分别表示△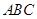 、△
、△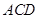 、△
、△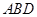 的面积,则
的面积,则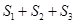 的最大值是 .
的最大值是 .
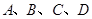 是半径为
是半径为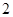 的球面上的四个不同点,且满足
的球面上的四个不同点,且满足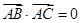 ,
,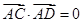 ,
,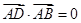 ,用
,用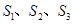 分别表示△
分别表示△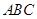 、△
、△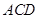 、△
、△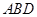 的面积,则
的面积,则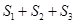 的最大值是 .
的最大值是 .8
解:设AB=a,AC=b,AD=c,
因为AB,AC,AD两两互相垂直,
扩展为长方体,它的对角线为球的直径,所以a2+b2+c2=4R2=16
S△ABC+S△ACD+S△ADB
=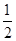 (ab+ac+bc )
(ab+ac+bc )
≤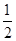 (a2+b2+c2)=8
(a2+b2+c2)=8
即最大值为:8
故答案为8.
因为AB,AC,AD两两互相垂直,
扩展为长方体,它的对角线为球的直径,所以a2+b2+c2=4R2=16
S△ABC+S△ACD+S△ADB
=
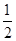 (ab+ac+bc )
(ab+ac+bc )≤
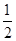 (a2+b2+c2)=8
(a2+b2+c2)=8即最大值为:8
故答案为8.

练习册系列答案
相关题目
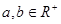 ,求证:
,求证: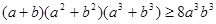 ;
;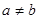 ,求证:
,求证: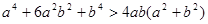
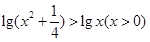
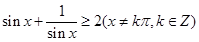
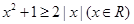

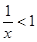 ;
;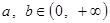 , 且
, 且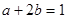 , 求
, 求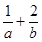 的最小值;
的最小值;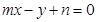 过点(2,1),其中
过点(2,1),其中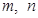 是正数,则
是正数,则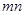 的最大值为
的最大值为
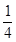
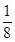

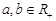 ,若
,若 ,则
,则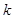 的最大值为 .
的最大值为 .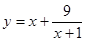 (
(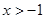 )的最小值
)的最小值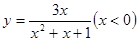 的值域是( )
的值域是( )