题目内容
曲线 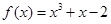 在点
在点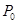 处的切线平行于直线
处的切线平行于直线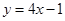 , 则点
, 则点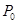 的坐标是()
的坐标是()
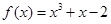 在点
在点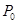 处的切线平行于直线
处的切线平行于直线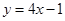 , 则点
, 则点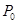 的坐标是()
的坐标是()A.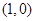 | B.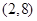 | C.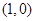 和 和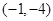 | D.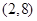 和 和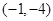 |
C
先设切点坐标,然后对f(x)进行求导,根据曲线在P0点处的切线平行于直线y=4x建立等式,从而求出切点的横坐标,代入到f(x)即可得到答案.
解答:解:设P0点的坐标为(a,f(a)),
由f(x)=x3+x-2,得到f′(x)=3x2+1,
由曲线在P0点处的切线平行于直线y=4x,得到切线方程的斜率为4,
即f′(a)=3a2+1=4,解得a=1或a=-1,
当a=1时,f(1)=0;当a=-1时,f(-1)=-4,
则P0点的坐标为(1,0)或(-1,-4).
故选C.
解答:解:设P0点的坐标为(a,f(a)),
由f(x)=x3+x-2,得到f′(x)=3x2+1,
由曲线在P0点处的切线平行于直线y=4x,得到切线方程的斜率为4,
即f′(a)=3a2+1=4,解得a=1或a=-1,
当a=1时,f(1)=0;当a=-1时,f(-1)=-4,
则P0点的坐标为(1,0)或(-1,-4).
故选C.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
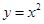 在点P处的切线的倾斜角为
在点P处的切线的倾斜角为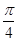 ,则P点坐标为 ( )
,则P点坐标为 ( )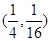
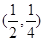
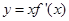 的图象如右图所示,(其中
的图象如右图所示,(其中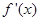 是函数
是函数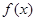 的导函数),则函数
的导函数),则函数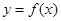 的大致图象是下图中的 ( )
的大致图象是下图中的 ( )
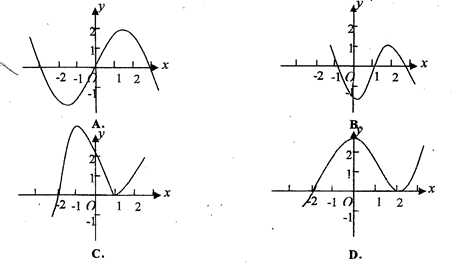
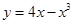 在点(-1,-3)处的切线方程是 ( )
在点(-1,-3)处的切线方程是 ( )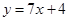 B
B 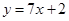 C
C 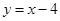 D
D 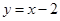
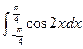 = 。
= 。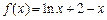 ,若
,若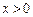 ,
,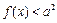 恒成立,则实数
恒成立,则实数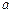 的取值范围是 .
的取值范围是 .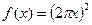 的导数是( )
的导数是( )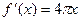
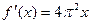
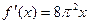
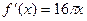
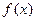 的二次项系数为a,且不等式
的二次项系数为a,且不等式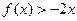 的解集为(1,3)。
的解集为(1,3)。 若方程
若方程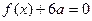 有两个相等的实数根,求
有两个相等的实数根,求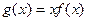 无极值,求实数
无极值,求实数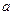 的取值范围。
的取值范围。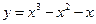 的单调增区间为______________________________。
的单调增区间为______________________________。