Question

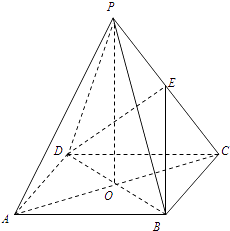
【题目】已知点G（5，4），圆C1：（x﹣1）2+（y﹣4）2=25，过点G的动直线l与圆C1 ， 相交于两点E、F，线段EF的中点为C． （Ⅰ）求点C的轨迹C2的方程；
（Ⅱ）若过点A（1，0）的直线l1：kx﹣y﹣k=0，与C2相交于两点P、Q，线段PQ的中点为M，l1与l2：x+2y+2=0的交点为N，求证：|AM||AN|为定值．

Answer 1

【答案】（Ⅰ）解：圆C1：（x﹣1）2+（y﹣4）2=25的圆心C1（1，4），半径为5，

设C（x，y），由圆的性质及勾股定理，

得（x﹣1）2+（y﹣4）2+（x﹣5）2+（y﹣4）2=（5﹣1）2+（4﹣4）2，

化简并整理，得（x﹣3）2+（y﹣4）2=4，∴点C的轨迹C2的方程为：（x﹣3）2+（y﹣4）2=4．

（Ⅱ）证明：∵过点A（1，0）的直线l1与C2相交于P、Q两点．

结合C2的方程（x﹣3）2+（y﹣4）2=4，知k≠0，

解方程组 ，得 ，

有直线C2M与l1垂直，∴C2M的方程为 ，

解 得， ，

则 ， ，

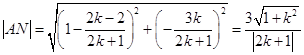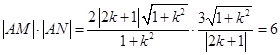∴ 为定值

【解析】（Ⅰ）设C（x，y），由圆的性质及勾股定理，得（x﹣1）2+（y﹣4）2+（x﹣5）2+（y﹣4）2=（5﹣1）2+（4﹣4）2，即可求点C的轨迹C2的方程；（Ⅱ）分别联立相应方程，求得M，N的坐标，再求：|AM||AN|为定值．