题目内容
行列式的运算定义为 =ad-bc,设i为虚数单位,则符合条件
=ad-bc,设i为虚数单位,则符合条件 =3-i的复数z= .
=3-i的复数z= .
【答案】分析:设出要求的复数,根据条件中定义的行列式,写出含有复数的行列式的结果,根据复数相等的充要条件,写出关于所设的复数的实部和虚部的关系式,即方程,解方程即可.
解答:解:设z=a+bi
∵行列式的运算定义为 =ad-bc,
=ad-bc,
∴ =3-i等价于z-zi=3-i,
=3-i等价于z-zi=3-i,
∴(a+bi)-(a+bi)i=3-i,
∴a+b+(b-a)i=3-i,
∴a+b=3,b-a=-1,
∴a=2,b=1,
∴z=2+i,
故答案为:2+i.
点评:本题是一个新定义问题,考查同学们的理解能力,考查复数相等的充要条件,是一个综合题,解题的关键是理解行列式的展开式.
解答:解:设z=a+bi
∵行列式的运算定义为
 =ad-bc,
=ad-bc,∴
 =3-i等价于z-zi=3-i,
=3-i等价于z-zi=3-i,∴(a+bi)-(a+bi)i=3-i,
∴a+b+(b-a)i=3-i,
∴a+b=3,b-a=-1,
∴a=2,b=1,
∴z=2+i,
故答案为:2+i.
点评:本题是一个新定义问题,考查同学们的理解能力,考查复数相等的充要条件,是一个综合题,解题的关键是理解行列式的展开式.

练习册系列答案
相关题目
 =ad-bc,设i为虚数单位,则符合条件
=ad-bc,设i为虚数单位,则符合条件 =3-i的复数z= .
=3-i的复数z= .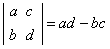 ,设i为虚数单位,则符合条件
,设i为虚数单位,则符合条件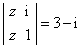 的复数z=( )。
的复数z=( )。