题目内容
26、已知△ABC中∠ACB=90°，SA⊥面ABC，AD⊥SC，求证：AD⊥面SBC．
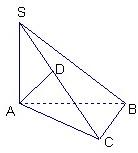
分析：要证线面垂直，关键要找到两条相交直线与之都垂直，先由线面垂直得线线垂直，然后利用线面垂直的判定得线面垂直继而得到线线垂直AD⊥BC，问题从而得证．
解答：证明：∵∠ACB=90°∴BC⊥AC（1分）
又SA⊥面ABC∴SA⊥BC（4分）
∴BC⊥面SAC（7分）
∴BC⊥AD（10分）
又SC⊥AD，SC∩BC=C∴AD⊥面SBC（12分）
又SA⊥面ABC∴SA⊥BC（4分）
∴BC⊥面SAC（7分）
∴BC⊥AD（10分）
又SC⊥AD，SC∩BC=C∴AD⊥面SBC（12分）
点评：本题考查了线面垂直的判定和线面垂直的定义的应用，考查了学生灵活进行垂直关系的转化，是个基础题．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
= ．