题目内容
已知△ABC中AC=4,AB=2若G为△ABC的重心,则 = .
= .
【答案】分析:由已知中△ABC中AC=4,AB=2若G为△ABC的重心,可得|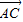 |=4,|
|=4,|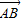 |=2,
|=2,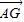 =
= (
(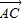 +
+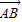 ),
),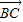 =
=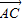 -
-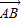 ,代入向量的数量积公式,可得答案.
,代入向量的数量积公式,可得答案.
解答:解:∵△ABC中AC=4,AB=2
∴|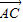 |=4,|
|=4,|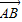 |=2
|=2
∵G为△ABC的重心,
∴ =
= (
(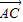 +
+ )
)
又∵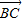 =
=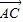 -
-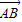
∴ =
= (
(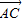 +
+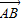 )•(
)•(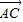 -
-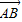 )=
)= (
(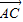 2-
2-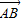 2)=
2)= (16-4)=4
(16-4)=4
故答案为:4
点评:本题考查的知识点是向量在几何中的应用,平面向量的数量积的运算,其中将已知条件转化为向量形式表示,是解答的关键.
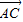 |=4,|
|=4,|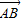 |=2,
|=2,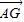 =
= (
(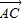 +
+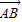 ),
),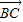 =
=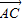 -
-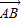 ,代入向量的数量积公式,可得答案.
,代入向量的数量积公式,可得答案.解答:解:∵△ABC中AC=4,AB=2
∴|
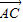 |=4,|
|=4,|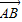 |=2
|=2∵G为△ABC的重心,
∴
 =
= (
(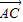 +
+ )
)又∵
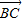 =
=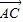 -
-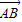
∴
 =
= (
(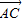 +
+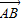 )•(
)•(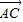 -
-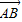 )=
)= (
(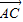 2-
2-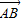 2)=
2)= (16-4)=4
(16-4)=4故答案为:4
点评:本题考查的知识点是向量在几何中的应用,平面向量的数量积的运算,其中将已知条件转化为向量形式表示,是解答的关键.

练习册系列答案
相关题目
