题目内容
已知角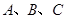 是
是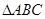 的内角,
的内角,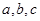 分别是其对边长,且
分别是其对边长,且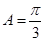 .
.
(1)若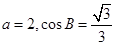 ,求
,求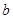 的长;
的长;
(2)设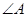 的对边
的对边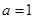 ,求
,求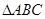 面积的最大值.
面积的最大值.
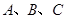 是
是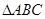 的内角,
的内角,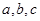 分别是其对边长,且
分别是其对边长,且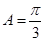 .
.(1)若
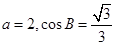 ,求
,求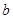 的长;
的长;(2)设
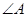 的对边
的对边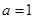 ,求
,求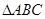 面积的最大值.
面积的最大值.(1)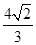 ;(2)
;(2)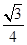 .
.
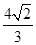 ;(2)
;(2)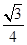 .
.试题分析:本题考查解三角形中的正弦定理和余弦定理的运用以及求三角形面积的最值,考查基本的运算能力.第一问,利用正弦定理求边长,先利用同角三角函数的平方关系求出
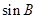 ,再用正弦定理;第二问,先利用余弦定理找到
,再用正弦定理;第二问,先利用余弦定理找到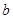 和
和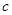 的关系,再利用基本不等式求
的关系,再利用基本不等式求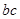 的范围,代入三角形面积公式中即可得到最大值.
的范围,代入三角形面积公式中即可得到最大值.试题解析: (1)在
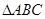 中,
中,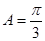 ,
,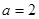 ,
,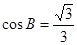
∴
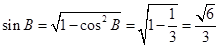
由正弦定理知:
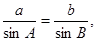
∴
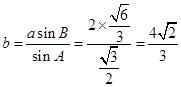 ,∴
,∴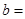
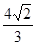
(2)当
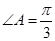 时,
时,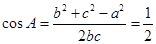
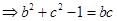 .
.又
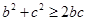 ,因此
,因此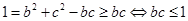 ,当且仅当
,当且仅当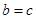 时等号成立.
时等号成立.所以
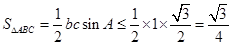 .故
.故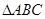 面积的最大为
面积的最大为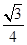 .
.
练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
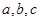 是
是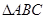 中
中 的对边,
的对边,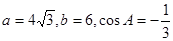 .
.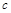 ;
;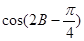 的值.
的值.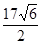 海里/小时
海里/小时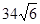 海里/小时
海里/小时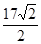 海里/小时
海里/小时 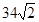 海里/小时
海里/小时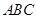 中,角
中,角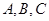 所对的边分别为
所对的边分别为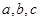 ,且
,且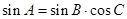 ,则
,则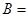 _______;若
_______;若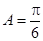 ,则
,则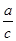
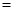 __________.
__________.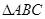 中,三内角
中,三内角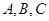 满足
满足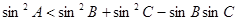 ,则角
,则角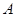 的取值范围为 .
的取值范围为 .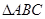 中,
中, 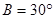 ,
,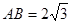 ,
,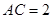 。则
。则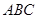 中,内角
中,内角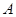 、
、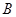 、
、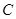 的对边分别为
的对边分别为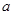 、
、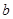 、
、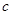 ,已知
,已知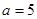 ,
,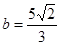 ,
,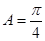 ,则
,则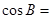 .
.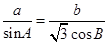 ,
,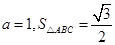 ,求b.
,求b.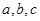 ,若
,若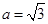 ,
,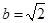 ,
,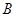 =45°,则角A=___.
=45°,则角A=___.