Question

若函数f(x)＝ax³－bx＋4，当x＝2时，函数f(x)有极值－.

(1)求函数的解析式；

(2)若关于x的方程f(x)＝k有三个零点，求实数k的取值范围。

Answer 1

【解析】由题意可知f′(x)＝3ax²－b，

(1)于是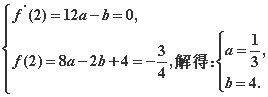

故所求的解析式为f(x)＝x³－4x＋4.

(2)由(1)可知f′(x)＝x²－4＝(x－2)(x＋2)，

令f′(x)＝0，得x＝2，或x＝－2.

当x变化时f′(x)、f(x)的变化情况如下表所示：

X	(－∞，－2)	－2	(－2,2)	2	(2，＋∞)
f′(x)	＋	0	－	0	＋
f(x)	单调递增		单调递减		单调递增

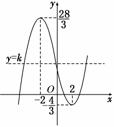
因此，当x＝－2时，f(x)有极大值；

当x＝2时，f(x)有极小值－.

所以函数的大致图象如图.故实数k的取值范围是－＜k＜.