题目内容
如果两个函数的对应关系相同,值域相同,但定义域不同,则这两个函数为“同族函数”,那么函数y=x2,x∈{1,2}的“同族函数”有( )
分析:利用同族函数的定义可知,只要其对应关系,值域相同,定义域不同即可,易得答案.
解答:解:∵函数y=x2,x∈{1,2}的值域为{1,4},所以对应关系是y=x2,值域为{1,4}的函数的定义域
可以是{-1,2},{1,-2},{-1,-2},{-1,1,2},{-1,1,-2},{2,1,-2},{2,-1,-2},{2,1,-1,-2}.
共8个.
故选C.
可以是{-1,2},{1,-2},{-1,-2},{-1,1,2},{-1,1,-2},{2,1,-2},{2,-1,-2},{2,1,-1,-2}.
共8个.
故选C.
点评:本题考查了函数的定义域,及函数的三要素,是个较基础的新定义题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
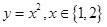 的“同族函数”有( )
的“同族函数”有( )