题目内容
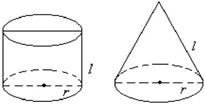15、①轴截面是正方形的圆柱叫等边圆柱．已知：等边圆柱的底面半径为r，求其全面积；
②轴截面是正三角形的圆锥叫等边圆锥．
已知：等边圆锥底面半径为r，求其全面积．
分析：①先根据等边圆柱的定义求出等边圆柱的母线长，代入圆柱的全面积的公式进行运算．
②先根据等边圆锥的而定义求出圆锥的母线长，代入圆锥的全面积公式进行运算．
②先根据等边圆锥的而定义求出圆锥的母线长，代入圆锥的全面积公式进行运算．
解答：解：①∵母线l=2r，
∴S侧=c•l=2πr•2r=4πr2，
∴S全=4πr2+2πr2 =6πr2．
②∵母线l=2r，
∴S侧 =πrl=πr•2r=2πr2，
∴S全 =2πr2+πr2 =3πr2．
∴S侧=c•l=2πr•2r=4πr2，
∴S全=4πr2+2πr2 =6πr2．
②∵母线l=2r，
∴S侧 =πrl=πr•2r=2πr2，
∴S全 =2πr2+πr2 =3πr2．
点评：本题考查等边圆柱、等边圆锥的定义和性质，圆柱、圆锥的全面积的运算方法．
练习册系列答案
相关题目
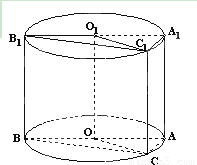
如图，轴截面为边长是2的正方形的圆柱OO1内有一个三棱柱ABC-A1B1C1，三棱柱的底面为圆柱底面的内接三角形，且AB是圆O的直径．∠AOC=60°
内有一个三棱柱
，三棱柱的底面为圆柱底面的内接三角形，且
是圆
的直径．
的体积；
⊥平面
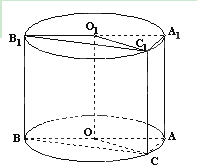如图，轴截面为边长是2的正方形的圆柱OO1内有一个三棱柱ABC-A1B1C1，三棱柱的底面为圆柱底面的内接三角形，且AB是圆O的直径．∠AOC=60°