题目内容
将函数 (
( )的图象绕坐标原点逆时针旋转
)的图象绕坐标原点逆时针旋转 (
( 为锐角),若所得曲线仍是一个函数的图象,则
为锐角),若所得曲线仍是一个函数的图象,则 的最大值为( )
的最大值为( )
A.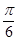 | B. | C.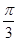 | D. |
C
解析试题分析:设f(x)= ,根据二次函数的单调性,可得函数在[0,1]上为增函数,在[1,2]上为减函数.
,根据二次函数的单调性,可得函数在[0,1]上为增函数,在[1,2]上为减函数.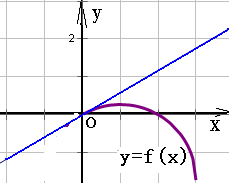
设函数在 x="0" 处,切线斜率为k,则k=f'(0)∵f'(x)=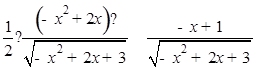 ,∴k=f'(0)=
,∴k=f'(0)=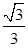 =tan30°,可得切线的倾斜角为 30°,因此,要使旋转后的图象仍为一个函数的图象,旋转θ后的切线倾斜角最多为 90°,也就是说,最大旋转角为 90°-30°=60°,即θ的最大值为60°,故答案为:C.
=tan30°,可得切线的倾斜角为 30°,因此,要使旋转后的图象仍为一个函数的图象,旋转θ后的切线倾斜角最多为 90°,也就是说,最大旋转角为 90°-30°=60°,即θ的最大值为60°,故答案为:C.
考点:函数的图象与图象变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义域为 的函数
的函数 (
( )有两个单调区间,则实数
)有两个单调区间,则实数 ,
, ,
, 满足( )
满足( )
A. 且 且 | B. | C. | D. |
给出以下命题:
①对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:“夹在两个平行平面间的平行线段相等”.
② =2;
=2;
③已知函数 的图象与直线
的图象与直线 有相异三个公共点,则
有相异三个公共点,则 的取值范围是(-2,2)
的取值范围是(-2,2)
其中正确命题是( )
| A.①②③ | B.①② | C.①③ | D.②③ |
函数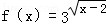 的值域为( )
的值域为( )
| A.[2,+∞) | B.[1,+∞) |
| C.(0,+∞) | D.(0,1] |
为了得到函数y=2x﹣3﹣1的图象,只需把函数y=2x上所有点( )
| A.向右平移3个单位长度,再向下平移1个单位长度 |
| B.向左平移3个单位长度,再向下平移1个单位长度 |
| C.向右平移3个单位长度,再向上平移1个单位长度 |
| D.向左平移3个单位长度,再向上平移1个单位长度 |
下列各组函数中表示同一函数的是( )
A.y= 和y= 和y= |
B.y=|x|和y= |
| C.y=logax2和y=2logax(a>0a≠1) |
| D.y=x和y=logaax(a>0,a≠1) |
若对任意x∈R,不等式|x|≥ax恒成立,则实数a的取值范围是( )
| A.a<﹣1 | B.|a|≤1 | C.|a|<1 | D.a≥1 |
 在定义域内的任意实数
在定义域内的任意实数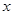 及
及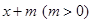 ,都有
,都有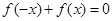 及
及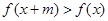 成立,则称函数
成立,则称函数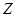 函数”.现给出下列四个函数:
函数”.现给出下列四个函数: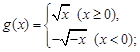
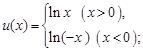
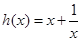 ;
;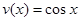 .其中是“
.其中是“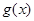
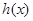
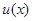
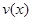
 其中
其中 表示不超过
表示不超过 的最大整数,(如
的最大整数,(如 ,
, ,
, ).若直线
).若直线 与函数
与函数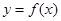 的图象恰有三个不同的交点,则实数
的图象恰有三个不同的交点,则实数 的取值范围是
的取值范围是 


