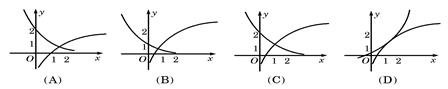题目内容
函数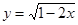 的定义域为集合A,函数
的定义域为集合A,函数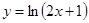 的定义域为B,则
的定义域为B,则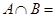
A.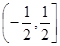 | B.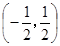 | C.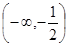 | D.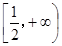 |
A
解析试题分析:由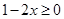 得,
得, ;由
;由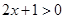 得,
得,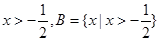 ,所以
,所以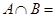
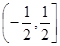 ,故选A.
,故选A.
考点:本题主要考查求函数定义域的方法,对数函数的性质,集合的运算。
点评:基础题,求函数的定义域,往往要建立不等式组,依据是“分母不为0,偶次根号下式子不小于0,对数的真数大于0”等等。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
已知函数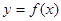 在R上是增函数,且
在R上是增函数,且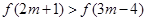 ,则
,则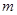 的取值范围是( )
的取值范围是( )
A.(-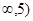 | B.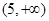 | C.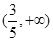 | D.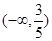 |
已知对任意实数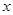 ,有
,有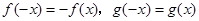 ,且
,且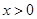 时
时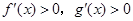 ,则
,则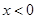 时( )
时( )
A.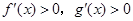 | B.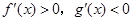 |
C.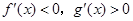 | D.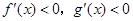 |
已知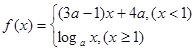 是(-
是(-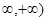 上的减函数,
上的减函数,
那么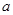 的取值范围是( )
的取值范围是( )
A.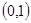 | B.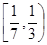 | C.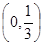 | D. |
已知函数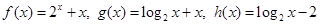 的零点依次为
的零点依次为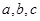 ,则( )
,则( )
A.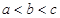 | B.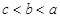 | C.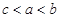 | D.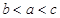 |
若函数 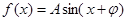 (A>0)在
(A>0)在 处取最大值,则 ( )
处取最大值,则 ( )
A.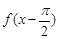 一定是奇函数 一定是奇函数 | B. 一定是偶函数 一定是偶函数 |
C. 一定是奇函数 一定是奇函数 | D. 一定是偶函数 一定是偶函数 |
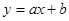 与
与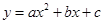 的图象关系可能正确的是( )
的图象关系可能正确的是( )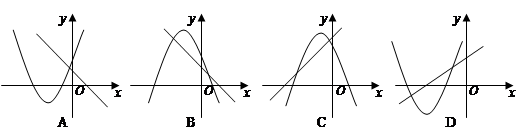
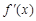 的图象如右图所示,那么函数f (x)的图象最有可能的是
的图象如右图所示,那么函数f (x)的图象最有可能的是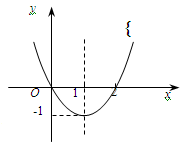
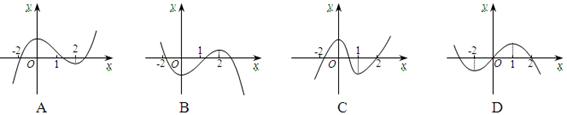
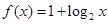 与
与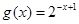 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )