题目内容
8.在极坐标系中,曲线ρ2-6ρcosθ-2ρsinθ+6=0与极轴交于A,B两点,则A,B两点间的距离等于( )| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{15}$ | D. | 4 |
分析 首先把极坐标方程转化成直角坐标方程,进一步利用在x轴上的两根和与两根积的关系式,利用两点间的距离公式求出结果.
解答 解:曲线ρ2-6ρcosθ-2ρsinθ+6=0转化成直角坐标方程为:
x2+y2-6x-2y+6=0.
由于曲线与极轴交于A,B两点,
设交点坐标为:A(x1,0),B(x2,0),
令y=0,则:x2-6x+6=0,
所以:x1+x2=6,x1x2=6.
则:|AB|=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{3}$.
故选:B
点评 本题考查的知识要点:极坐标方程与直角坐标方程的互化,两点间的距离公式的应用,及相关的运算问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知集合 A={1,2,m2},B={1,m}.若B⊆A,则m=( )
| A. | 0 | B. | 2 | C. | 0 或2 | D. | 1 或2 |
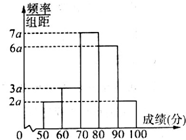 100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则测试成绩落在[60,80)中的学生人数是50.
100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则测试成绩落在[60,80)中的学生人数是50.