题目内容
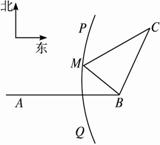
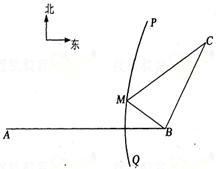
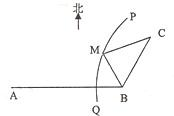 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元∕km、2a万元/km,那么修建这两条公路的总费用最低是
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元∕km、2a万元/km,那么修建这两条公路的总费用最低是分析:依题意知曲线PQ是以A、B为焦点、实轴长为2的双曲线的一支,此双曲线的离心率为2,以直线AB为x轴、AB的中点为原点建立平面直角坐标系,则该双曲线的方程为x2-
=1,点C的坐标为(3,
).求出修建这条公路的总费用W,根据双曲线的定义有|MM1|=
|MB|,根据a+b≥2
当且仅当a=b时取等号的方法求出W的最小值即可.
| y2 |
| 3 |
| 3 |
| 1 |
| 2 |
| ab |
解答:解:依题意知曲线PQ是以A、B为焦点、实轴长为2的双曲线的一支,此双曲线的离心率为2,以直线AB为x轴、AB的中点为原点建立平面直角坐标系,则该双曲线的方程为x2-
=1,点C的坐标为(3,
).则修建这条公路的总费用W=a|MB|+2a|MC|=2a(
|MB|+|MC|),设点M、C在双曲线右准线上射影分别为点M1、C1,根据双曲线的定义有|MM1|=
|MB|,所以W=2a(
|MB|+|MC|)=2a(|MM1|+MC|)≥2a|CC1|=2a×(3-
)=5a
当且仅当点M为曲线PQ与线段CC1的交点时取等号,故W的最小值是5a.
故答案为;5a.
| y2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当点M为曲线PQ与线段CC1的交点时取等号,故W的最小值是5a.
故答案为;5a.
点评:考查学生根据实际问题选择函数类型的能力,以及会用a+b≥2
当且仅当a=b时取等号的方法来求函数的最小值的能力.
| ab |

练习册系列答案
相关题目
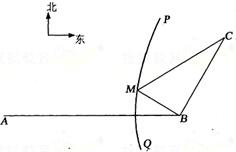 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的没岸PQ(曲线)上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km,那么修建这两条公路的总费用最低是( )
A、(2
| ||
| B、5a万元 | ||
C、(2
| ||
D、(2
|
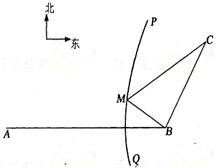 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km..现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.那么这两条公路MB、MC的路程之和最短是
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km..现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.那么这两条公路MB、MC的路程之和最短是