题目内容
已知中心在原点,其中一个焦点为F(-1,0)的椭圆经过点P(
,-
),椭圆的右顶点为A,经过点F的直线l与椭圆交于两点B,C.
(1)求椭圆的方程;
(2)若△ABC的面积为
,求直线l的方程.
| 2 |
| ||
| 2 |
(1)求椭圆的方程;
(2)若△ABC的面积为
| 18 |
| 7 |
| 2 |
(1)设椭圆的方程为:
+
=1 (a>b>0)(1分)
由题设知
,解得:
(5分)
因此,椭圆的方程为:
+
=1.(6分)
(2)若直线l⊥x轴,则l的方程为:x=-1,
此时B、C的坐标为(-1,
)、(-1,-
).
由于点A的坐标为(2,0),则△ABC的面积为
.不合题意,舍去:(7分)
若直线l不与x轴垂直,可设l的方程为:y=k(x+1).
则直线与椭圆恒有两交点.
由
,得:(3+4k2)x2+8k2x+4k2-12=0(8分)
记B(x1,y1)、C(x2,y2),则有
,(9分)
由于|BC|=
=
点A到直线l的距离为
,(11分)
将上面两式代入△ABC的面积公式可得:
•
•
=
,(12分)
整理得:17k4+k2-18=0(13分)
解得:k2=-
(舍去),k2=1故k=±1,
从而,直线l的方程为:y=±(x+1).(14分)
| x2 |
| a2 |
| y2 |
| b2 |
由题设知
|
|
因此,椭圆的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)若直线l⊥x轴,则l的方程为:x=-1,
此时B、C的坐标为(-1,
| 3 |
| 2 |
| 3 |
| 2 |
由于点A的坐标为(2,0),则△ABC的面积为
| 9 |
| 2 |
若直线l不与x轴垂直,可设l的方程为:y=k(x+1).
则直线与椭圆恒有两交点.
由
|
记B(x1,y1)、C(x2,y2),则有
|
由于|BC|=
| (1+k2)[(x1+x2)2-4x1x2] |
| 12(1+k2) |
| 3+4k2 |
点A到直线l的距离为
| |3k| | ||
|
将上面两式代入△ABC的面积公式可得:
| 1 |
| 2 |
| 12(1+k2) |
| 3+4k2 |
| |3k| | ||
|
| 18 |
| 7 |
| 2 |
整理得:17k4+k2-18=0(13分)
解得:k2=-
| 18 |
| 7 |
从而,直线l的方程为:y=±(x+1).(14分)

练习册系列答案
相关题目
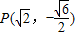 ,椭圆的右顶点为A,经过点F的直线l与椭圆交于两点B,C.
,椭圆的右顶点为A,经过点F的直线l与椭圆交于两点B,C.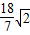 ,求直线l的方程.
,求直线l的方程.