题目内容
10.设集合A={x|x=2t2+4t+1},B={y|y=-3x2+6x+10},则A∩B=[-1,13].分析 利用配方法求出集合A={x|x≥-1},B={y|y≤13},由此能求出A∩B的值.
解答 解:∵集合A={x|x=2t2+4t+1}={x|x=2(t+1)2-1≥-1},
B={y|y=-3x2+6x+10}={y|y=-3(x-1)2+13≤13},
∴A∩B=[-1,13].
故答案为:[-1,13].
点评 本题考查集合的交集的求法,是基础题,解题时要注意配方法的合理运用.

练习册系列答案
相关题目
18.设函数f(x)=x2+3x-5lnx,则f(x)的递减区间为( )
| A. | (-$\frac{5}{2}$,1) | B. | (-∞,-$\frac{5}{2}$),(1,+∞) | C. | (1,+∞) | D. | (0,1) |
7.若f′(x0)=3,则$\underset{lim}{h→0}\frac{f({x}_{0}-2h)-f({x}_{0}+h)}{6h}$等于( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
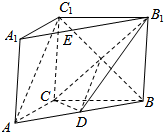 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=2$\sqrt{3}$,AA1=2,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=2$\sqrt{3}$,AA1=2,点D是AB的中点.