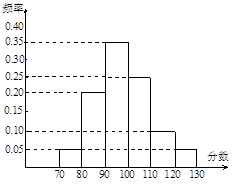题目内容
空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定。空气质量指数越高,代表空气污染越严重:
| 空气质量指数 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | ≥250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |

(1)估计某市一个月内空气受到污染的概率(规定:空气质量指数大于或等于75,空气受到污染);
(2)在空气质量类别为“良”、“轻度污染”、“中度污染”的监测数据中用分层抽样方法抽取一个容量为6的样本,若在这6数据中任取2个数据,求这2个数据所对应的空气质量类别不都是轻度污染的概率.
(1)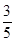 ;(2)
;(2) .
.
解析试题分析:(1)由条形统计图可知,空气质量类别为受到污染的天数为18天,从而可求此次监测结果中空气质量类别为良的概率;
(2)样本中空气质量级别为“良”、“轻度污染”、“中度污染”分别有8、16、4天,由分层抽样方法抽取“良”、“轻度污染”、“中度污染”的监测数据的分别为2,3,1,设它们的数据依次为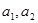 、
、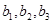 、
、 ,则抽取2天数据的基本事件总数为
,则抽取2天数据的基本事件总数为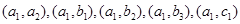 ,
,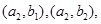
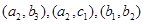



 共15种,设这2天的空气质量类别不都是轻度污染为事件A,则A中的基本事件数为12种,所以
共15种,设这2天的空气质量类别不都是轻度污染为事件A,则A中的基本事件数为12种,所以 ,即这2天的空气质量类别都不是轻度污染的概率为
,即这2天的空气质量类别都不是轻度污染的概率为 .
.
试题解析:(1) 由互斥事件概率关系得空气受到污染的概率 5分
5分
(2)由分层抽样方法抽取“良”、“轻度污染”、“中度污染”的监测数据的分别为2,3,1 7分
设它们的数据依次为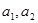 、
、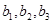 、
、 ,则抽取2天数据的基本事件总数为
,则抽取2天数据的基本事件总数为 ,
,
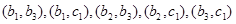 共15种 9分
共15种 9分
设这2天的空气质量类别不都是轻度污染为事件A,则A中的基本事件数为12种
所以 ,即这2天的空气质量类别都不是轻度污染的概率为
,即这2天的空气质量类别都不是轻度污染的概率为 12分
12分
考点:1.条形图应用;2.古典概型.

甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
(2)若规定考试成绩在[120,150]内为优秀,请分别估计两所学校数学成绩的优秀率;
(3)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.10的前提下认为两所学校的数学成绩有差异.
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
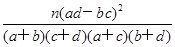 . ?
. ?临界值表
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
从某校高二年级 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到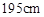 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组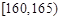 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
| 分组 | 频数 | 频率 | 频率/组距 |
| | | | |
 |  | 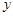 |  |
 |  |  |  |
| | | | |

(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取
 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率.  =40
=40
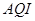 技术规定》(试行),
技术规定》(试行),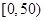 为优,
为优, 为良,
为良,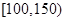 为轻度污染,
为轻度污染,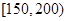 为中度污染,
为中度污染,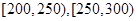 均为重度污染,
均为重度污染,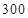 及以上为严重污染.某市2013年11月份
及以上为严重污染.某市2013年11月份 天的
天的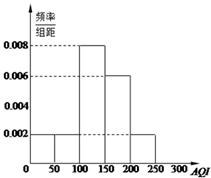
 天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天? 时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少? 表示.
表示.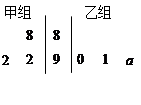
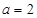 时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.