题目内容
11．A，B，C是球O上的三点，AB=10，AC=6，BC=8，球O的半径等于13，求球心O到平面ABC的距离．分析 先确定△ABC的形状为Rt△，然后找出球心到平面ABC的距离，求解即可．
解答 解：∵62+82=102，∴△ABC为Rt△．
∵球心O在平面ABC内的射影M是截面圆的圆心，
∴M是AC的中点且OM⊥AC．
在Rt△OAM中，OM=$\sqrt{1{3}^{2}-{5}^{2}}$=12．
∴球心到平面ABC的距离为12．
点评 本题考查球的有关计算问题，点到平面的距离，是基础题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
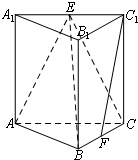如图，在三棱柱ABC-A1B1C1中，侧棱垂直于底面，AB⊥BC，E、F分别为A1C1、BC的中点．
3．设集合A={x|-1≤x≤2}，B={x|0≤x≤4}，则A∪B=（ ）
| A． | {x|0≤x≤2} | B． | {x|1≤x≤2} | C． | {x|0≤x≤4} | D． | {x|-1≤x≤4} |