题目内容
若函数 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 是等比源函数.
是等比源函数.
(Ⅰ)判断下列函数:① ;②
;② ;③
;③ 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(Ⅱ)判断函数 是否为等比源函数,并证明你的结论;
是否为等比源函数,并证明你的结论;
(Ⅲ)证明: ,函数
,函数 都是等比源函数.
都是等比源函数.
(Ⅰ)①②③(Ⅱ)不是等比源函数(Ⅲ)略
解析试题分析:(Ⅰ)① 是等比源函数,例:当
是等比源函数,例:当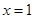 时,
时,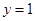 ;当
;当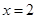 时,
时,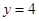 ;当
;当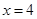 时,
时,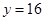 。1、4、16成等比。②
。1、4、16成等比。② 是等比源函数,例:当
是等比源函数,例:当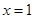 时,
时,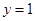 ;当
;当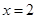 时,
时,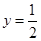 ;当
;当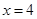 时,
时,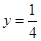 。
。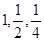 成等比。③
成等比。③ 是等比源函数,例:当
是等比源函数,例:当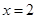 时,
时,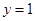 ;当
;当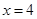 时,
时,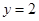 ;当
;当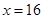 时,
时,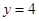 。1、2、4成等比数列。(Ⅱ)假设函数
。1、2、4成等比数列。(Ⅱ)假设函数 是等比源函数,即存在正整数
是等比源函数,即存在正整数 且
且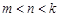 ,使得
,使得 成等比数列,根据等比中项列出式子,再推理论证得出矛盾。(Ⅲ)根据
成等比数列,根据等比中项列出式子,再推理论证得出矛盾。(Ⅲ)根据 可推导出
可推导出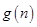 为首项为正整数公差也为正整数的等差数列。假设
为首项为正整数公差也为正整数的等差数列。假设 (
(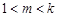 )整理得
)整理得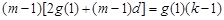 当
当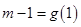 时说明假设成立,即函数
时说明假设成立,即函数 值中存在三个不同的数构成等比数列。
值中存在三个不同的数构成等比数列。
试题解析:(Ⅰ)①②③都是等比源函数. 3分
(Ⅱ)函数 不是等比源函数. 4分
不是等比源函数. 4分
证明如下:
假设存在正整数 且
且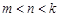 ,使得
,使得 成等比数列,
成等比数列,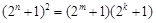 ,整理得
,整理得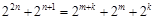 , 5分
, 5分
等式两边同除以 得
得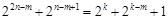 .
.
因为 ,所以等式左边为偶数,等式右边为奇数,
,所以等式左边为偶数,等式右边为奇数,
所以等式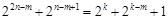 不可能成立,
不可能成立,
所以假设不成立,说明函数 不是等比源函数. 8分
不是等比源函数. 8分
(Ⅲ)法1:
因为 ,都有
,都有 ,
,
所以 ,数列
,数列 都是以
都是以 为首项公差为
为首项公差为 的等差数列.
的等差数列. ,
,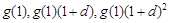 成等比数列,
成等比数列,
因为 ,
, ,
,
所以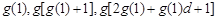
 ,
,
所以 ,函数
,函数 都是等比源函数. 13分
都是等比源函数. 13分
(Ⅲ)法2:
因为 ,都有
,都有 ,
,
所以 ,数列
,数列 都是以
都是以 为首项公差为
为首项公差为 的等差数列.
的等差数列.
由 ,(其中
,(其中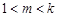 )可得
)可得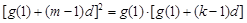 ,整理得
,整理得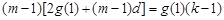 ,
,
令 ,则
,则 ,
,
所以
练习册系列答案
相关题目

 ,求实数m的值;
,求实数m的值; ,求实数m的取值范围。
,求实数m的取值范围。 ,求实数a的取值范围.
,求实数a的取值范围.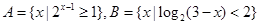 ,求
,求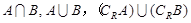 .
. 的值域,集合C为不等式
的值域,集合C为不等式 (x+4)≤0的解集.
(x+4)≤0的解集.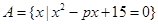 ,
,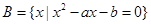 ,
,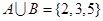 ,
,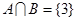 ,求
,求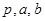 的值.
的值.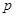 :实数
:实数 满足
满足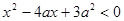 ,其中
,其中 ;命题
;命题 :实数
:实数 且
且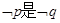 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.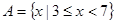 ,
,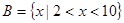 ,
,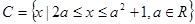 。
。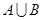 ,
,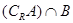 ;
;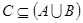 ,求实数
,求实数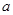 的取值范围.
的取值范围. 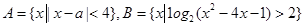
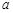 =l,求
=l,求 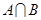 ;
;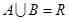 ,求实数
,求实数