题目内容
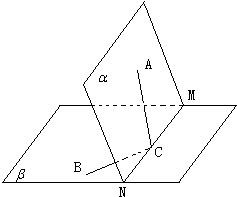 如图,已知平面α∩平面β=MN,A∈α,B∈β,C∈MN且∠ACM=60°,∠BCN=45°,二面角A-MN-B=60°,AC=2.
如图,已知平面α∩平面β=MN,A∈α,B∈β,C∈MN且∠ACM=60°,∠BCN=45°,二面角A-MN-B=60°,AC=2.(Ⅰ)求点A到平面β的距离;
(Ⅱ)设二面角A-BC-M的大小为θ,求tanθ的值.
分析:(I)由题意及图形作AO⊥β于O,AD⊥AN于D,连接OD,知∠ADO=60°,然后在直角三角形中求解即可;
(II)如图,在β平面内,过点O作直线BC的垂线,垂足为F,与直线MN交于E点,∠AOF为二面角A-BC-M的平面角,然后再三角形中求解即可.
(II)如图,在β平面内,过点O作直线BC的垂线,垂足为F,与直线MN交于E点,∠AOF为二面角A-BC-M的平面角,然后再三角形中求解即可.
解答: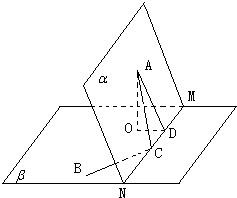 解:(Ⅰ)如图,
解:(Ⅰ)如图,
作AO⊥β于O,AD⊥AN于D,连接OD,知∠ADO=60°,
在Rt△ADC中,易得AD=
CD=1,在Rt△ADO中,OD=
,AO=
×sin60°=
.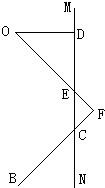
(Ⅱ)如图,在β平面内,过点O作直线BC的垂线,垂足为F,与直线MN交于E点,
易证∠AOF为二面角A-BC-M的平面角,
由已知得∠BCN=∠ECF=∠CEF=45°,
可求得OE=
,DE=DO=
,EC=1-
,EF=
×(1-
) =
,OF=OE+EF=
+
=
,
tanθ=
=
=
-
.
 解:(Ⅰ)如图,
解:(Ⅰ)如图,作AO⊥β于O,AD⊥AN于D,连接OD,知∠ADO=60°,
在Rt△ADC中,易得AD=
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |

(Ⅱ)如图,在β平面内,过点O作直线BC的垂线,垂足为F,与直线MN交于E点,
易证∠AOF为二面角A-BC-M的平面角,
由已知得∠BCN=∠ECF=∠CEF=45°,
可求得OE=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| |||||
| 4 |
| ||
| 2 |
| |||||
| 4 |
| |||||
| 4 |
tanθ=
| AO |
| OF |
| |||||||
|
| 6 | 2 |
| 3 | 6 |
点评:此题重点考查了利用二面角平面角的概念及在三角形中求解角的大小,还考查了学生的空间想象能力及计算能力.

练习册系列答案
相关题目
 9、如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
9、如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
 如图,已知直角梯ACDE所在的平面垂直于平ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯ACDE所在的平面垂直于平ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
