题目内容
数列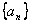 的前n项和为Sn=2n-1。
的前n项和为Sn=2n-1。
(1)求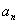 ;
;
(2)设数列 满足
满足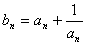 ,判断并证明
,判断并证明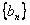 的单调性;
的单调性;
(3)对n∈N*,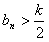 恒成立,求k的最大整数值。
恒成立,求k的最大整数值。
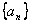 的前n项和为Sn=2n-1。
的前n项和为Sn=2n-1。(1)求
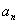 ;
;(2)设数列
 满足
满足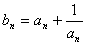 ,判断并证明
,判断并证明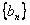 的单调性;
的单调性;(3)对n∈N*,
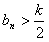 恒成立,求k的最大整数值。
恒成立,求k的最大整数值。 解:(1) ;
;
(2)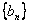 为递增数列;
为递增数列;
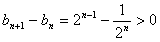 ;
;
(3)k的最大整数值为3。
 ;
;(2)
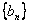 为递增数列;
为递增数列;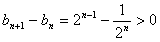 ;
;(3)k的最大整数值为3。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
