题目内容
甲、乙、丙三人分别独立解一道数学题,已知甲做对这道题的概率是| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
(1)求乙、丙两人各自做对这道题的概率;
(2)求做对该题人数随机变量ξ的分布列和Eξ.
分析:本题考查的知识点有:等可能事件的概率,离散型随机变量及其分布列、期望与方差,是一道相对综合的概率问题,
(1)我们根据甲做对这道题的概率是
,甲、丙两人都做错的概率是
,乙、丙两人都做对的概率是
.不难构造方程组,求出乙和丙做对该题的概率.
(2)根据(1)的结论,根据分布列及数学期望的计算公式,易得到最终结果.
(1)我们根据甲做对这道题的概率是
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
(2)根据(1)的结论,根据分布列及数学期望的计算公式,易得到最终结果.
解答:解:记甲、乙、丙三人独立做对这道题的事件依次为A、B、C,
则由已知条件得:P(A)=
又∵P(
•
)=[1-P(A)][1-P(C)]=
,∴P(C)=
又∵P(B•C)=P(B)•P(C)=
,∴P(B)=
乙、丙三人各自做对这道题的概率分别为
,
(2)随机变量ξ的可能值为0,1,2,3,则
P(ξ=0)=P(
)P(
)P(
)=
×
×
=
P(ξ=1)=P(A)P(
)P(
)+P(
)P(B)P(
)+P(
)P(
)P(C)=
P(ξ=2)=P(A)P(B)P(
)+P(
)P(B)P(C)+P(A)P(
)P(C)=
P(ξ=3)=P(A)P(B)P(C)=
∴ξ的分布列为:
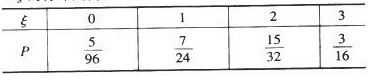
∴Eξ=0×
+1×
+2×
+3×
=
则由已知条件得:P(A)=
| 3 |
| 4 |
又∵P(
. |
| A |
. |
| C |
| 1 |
| 12 |
| 2 |
| 3 |
又∵P(B•C)=P(B)•P(C)=
| 1 |
| 4 |
| 3 |
| 8 |
乙、丙三人各自做对这道题的概率分别为
| 3 |
| 8 |
| 2 |
| 3 |
(2)随机变量ξ的可能值为0,1,2,3,则
P(ξ=0)=P(
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 4 |
| 5 |
| 8 |
| 1 |
| 3 |
| 5 |
| 96 |
P(ξ=1)=P(A)P(
. |
| B |
. |
| C |
. |
| A |
. |
| C |
. |
| A |
. |
| B |
| 7 |
| 24 |
P(ξ=2)=P(A)P(B)P(
. |
| C |
. |
| A |
. |
| B |
| 15 |
| 32 |
P(ξ=3)=P(A)P(B)P(C)=
| 3 |
| 16 |
∴ξ的分布列为:

∴Eξ=0×
| 5 |
| 96 |
| 7 |
| 24 |
| 15 |
| 32 |
| 3 |
| 16 |
| 24 |
| 43 |
点评:若A事件发生的概率为P(A),B事件发生的概率为P(B),则
①A,B同时发生的概率为P(A)P(B);
②A,B同时不发生的概率为P(
)P(
);
③A不发生B发生的概率为P(
)P(B);
④A发生B不发生的概率为P(A)P(
);
①A,B同时发生的概率为P(A)P(B);
②A,B同时不发生的概率为P(
. |
| A |
. |
| B |
③A不发生B发生的概率为P(
. |
| A |
④A发生B不发生的概率为P(A)P(
. |
| B |

练习册系列答案
相关题目
 ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是 ,甲、乙、丙全部做错的概率是
,甲、乙、丙全部做错的概率是 .
. ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是 ,甲、乙、丙三人全做错的概率是
,甲、乙、丙三人全做错的概率是 .
.