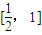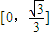题目内容
已知y=kx+2k+1,当-1≤x≤1时,y的值有正也有负,则k的取值范围是( )
| A、k<0或k>1 | ||
| B、0<k<1 | ||
C、-1<k<-
| ||
D、k<-1或k>-
|
分析:由题意,当-1≤x≤1时,y的值有正也有负,即f(-1)•f(1)<0,代入求出k的取值范围.
解答:解:∵y=f(x)=kx+2k+1,当-1≤x≤1时,y的值有正也有负,
∴f(-1)•f(1)<0,
即(-k+2k+1)•(k+2k+1)<0,
∴(k+1)•(3k+1)<0
解得-1<k<-
;
∴k的取值范围是{k|-1<k<-
};
故选:C.
∴f(-1)•f(1)<0,
即(-k+2k+1)•(k+2k+1)<0,
∴(k+1)•(3k+1)<0
解得-1<k<-
| 1 |
| 3 |
∴k的取值范围是{k|-1<k<-
| 1 |
| 3 |
故选:C.
点评:本题考查了一次函数的图象与性质,解题时结合图形,容易解得答案,是基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
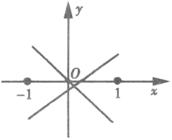 D.k<-1或k>-
D.k<-1或k>-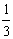
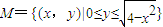 ,直线l:y=kx+2k与曲线C:
,直线l:y=kx+2k与曲线C: 有两个不同的交点,设直线l与曲线C围成的封闭区域为P,在区域M内随机取一点A,点A落在区域P内的概率为p,若
有两个不同的交点,设直线l与曲线C围成的封闭区域为P,在区域M内随机取一点A,点A落在区域P内的概率为p,若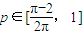 ,则实数k的取值范围为( )
,则实数k的取值范围为( )