题目内容
已知数列{xn}的首项x1=3，通项xn=2np+nq（n∈N+，p、q为常数）且x1，x4，x5成等差数列．
（1）求p、q的值；
（2）{xn}前n项和为Sn，计算S10的值．
解：（1）由x1=3，则3=2p+q①，
又x1，x4，x5成等差数列，
则（3+32p+5q）=2（16p+4q）②，
联立①②，解得p=1，q=1；
（2）把p=1，q=1代入通项得：xn=2n+n，
则S10=2+22+…+210+1+2+…+10=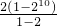
+
=2101．
分析：（1）把n=1代入通项其值等于3，得到关于p与q的方程，记作①，又令n=4和5分别表示出x4和x5，根据x1，x4，x5成等差数列，利用等差数列的性质得到2x4=x1+x5，列出关于p与q的另一方程，记作②，联立①②即可求出p与q的值，；
（2）把p与q的值代入通项即可确定出通项，罗列出数列{xn}的前10项，依次结合后，分别利用等比数列和等差数列的前n项和公式即可求出S10的值．
点评：此题考查学生掌握等差数列的性质，灵活运用等差数列及等比数列的前n项和公式化简求值，是一道中档题．
又x1，x4，x5成等差数列，
则（3+32p+5q）=2（16p+4q）②，
联立①②，解得p=1，q=1；
（2）把p=1，q=1代入通项得：xn=2n+n，
则S10=2+22+…+210+1+2+…+10=
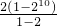+=2101．分析：（1）把n=1代入通项其值等于3，得到关于p与q的方程，记作①，又令n=4和5分别表示出x4和x5，根据x1，x4，x5成等差数列，利用等差数列的性质得到2x4=x1+x5，列出关于p与q的另一方程，记作②，联立①②即可求出p与q的值，；
（2）把p与q的值代入通项即可确定出通项，罗列出数列{xn}的前10项，依次结合后，分别利用等比数列和等差数列的前n项和公式即可求出S10的值．
点评：此题考查学生掌握等差数列的性质，灵活运用等差数列及等比数列的前n项和公式化简求值，是一道中档题．
练习册系列答案
相关题目
(n∈N+，p、q为常数)且x1,x4,x5成等差数列.