题目内容
已知二项式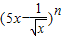 展开式中各项系数之和比各二项式系数之和大240,
展开式中各项系数之和比各二项式系数之和大240,(1)求n;
(2)求展开式中含x项的系数;
(3)求展开式中所有x的有理项.
【答案】分析:(1)由于各项系数之和为M=4n,二项式系数之和为N=2n,M-N=240=4n-2n,解方程求得 n 的值.
(2)利用二项展开式的通项公式写出第r+1项,令x的指数为1得到系数,得到结果.
(3)根据第二问写出的结果,使得x的指数是整数,列举出有三个结果,写出这几项即可.
解答:解:(1)由已知得:4n-2n=240,2n=16,n=4…(3分)
(2)通项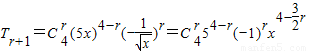 ,
,
令
所以含x项的系数:C4252(-1)2=150…(8分)
(3)由(2)得: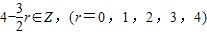 ,即r=0,2,4
,即r=0,2,4
所以展开式中所有x的有理项为:T1=625x4,T3=150x,T5=x-2…(13分)
点评:本题考查各项系数之和,与二项式系数之和的关系,得到 各项系数之和为M=4n,二项式系数之和为N=2n,是解题的关键.
(2)利用二项展开式的通项公式写出第r+1项,令x的指数为1得到系数,得到结果.
(3)根据第二问写出的结果,使得x的指数是整数,列举出有三个结果,写出这几项即可.
解答:解:(1)由已知得:4n-2n=240,2n=16,n=4…(3分)
(2)通项
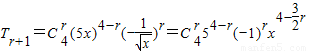 ,
,令

所以含x项的系数:C4252(-1)2=150…(8分)
(3)由(2)得:
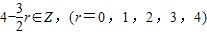 ,即r=0,2,4
,即r=0,2,4所以展开式中所有x的有理项为:T1=625x4,T3=150x,T5=x-2…(13分)
点评:本题考查各项系数之和,与二项式系数之和的关系,得到 各项系数之和为M=4n,二项式系数之和为N=2n,是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
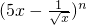 展开式中各项系数之和比各二项式系数之和大240,
展开式中各项系数之和比各二项式系数之和大240, 展开式中各项系数之和比各二项式系数之和大240,(1)求n; (2)求展开式中含
展开式中各项系数之和比各二项式系数之和大240,(1)求n; (2)求展开式中含